Question

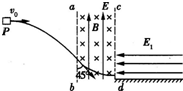如图所示，空间存在垂直纸面向里的匀强磁场和竖直向上的匀强电场，电磁场竖直边界ab、cd间的距离为L．现有质量为m、带电荷量为+q的小滑块从P点以v₀的速度水平飞出，随后与ab成45°角射入电磁场中，电场强度大小为E=

mg

q

．若小滑块垂直cd边界飞出电磁场，且恰能进入右边的光滑水平绝缘台面上，台面上方空间存在水平向左的匀强电场，场强大小为E₁．求：
（1）小滑块进入磁场时的速度大小；
（2）匀强磁场的磁感应强度B的大小；
（3）小滑块在光滑水平绝缘台面向右滑行的最大距离s与对应的时间t．

Answer 1

分析：（1）根据运动的分解与合成，结合平抛运动的特征，即可求解；
（2）根据牛顿第二定律，与几何关系，从而即可求解；
（3）根据动能定理，求出发生的位移；再由运动学公式与牛顿第二定律，即可求解．

解答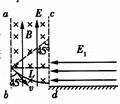：解：（1）小滑块从P点到刚进入磁场过程做平抛运动，
则小滑块进入磁场时的速度为，v=

v0

sin45°

=

2

v0
（2）因为有E=

mg

q

，所以小滑块在电磁场中做匀速圆周运动，设其轨道半径为R，
由几何关系可知，R=

L

sin45°

=

2

L
又有 qvB=m

v2

R

，
解得：B=

mv0

qL

（3）小滑块进入水平绝缘台面后，由动能定理，则有：
-qE1s=0-

1

2

mv2
解得：s=

m v 2 0

qE1

小滑块向右滑行的最大距离对应的时间
t=

v

a

，
又有a=

qE1

m

 联立解得：t=

2 mv0

qE1

答：
（1）小滑块进入磁场时的速度大小

2

v0；
（2）匀强磁场的磁感应强度B的大小

mv0

qL

；
（3）小滑块在光滑水平绝缘台面向右滑行的最大距离为

m v 2 0

qE1

与对应的时间

2 mv0

qE1

．

点评：考查牛顿第二定律、运动学公式与动能定理等规律的应用，掌握平抛运动的处理规律，理解动能定理的过程确定的重要性．会用几何知识解决电磁偏转的问题．