题目内容
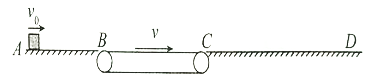
【题目】如图所示，一质量为m的小物体（可视为质点）以某一速度v0滑上一水平轨道ABCD， AB段光滑，BC段为水平传送带，CD段为足够长粗糙平面，三段轨道无缝连接．传送带BC段长度L =lOm，在皮带轮带动下始终以v=3m/s的速度向右匀速运动，已知物体与传送带之间的动摩擦因数为u1=0.2，物体与粗糙平面CD之间动摩擦因数为u2=0.3，g取l0m/s2，求：
(1)当v0=2m/s时，物体在CD段上滑行的距离；
(2)当v0=5m/s时，物体通过传送带后，在传送带上留下的划痕长度；
(3)速度v0在何范围内时，物体离开传送带后能到达同一位置。
【答案】（1）
（2）
（3）
【解析】试题分析：根据匀变速直线运动的规律求解匀加速的位移，从而知在CD的初速度，再根据速度位移关系知CD上距离；根据速度时间关系求共速的时间，根据时间求位移，从而知位移之差；物体离开传送带后能到达同一位置，则说明末速度一样都为3m/s，根据速度位移关系求解初速度的范围。
（1）根据牛顿运动定律： 
，解得BC加速度大小为： 
，当v0=2m/s时，与传送带速度相同运动的位移
，
代入数据解得：x1=1.25m＜L=10m，故滑上CD初速度为3m/s
同理可得：CD段加速度大小a2=μ2g=3m/s2，在CD上滑行距离： 
代入数据解得： 
（2）当v0=5m/s时，物体通过传送带后，当v0=2m/s时
与传送带速度相同运动的位移且为： 
代入数据解得：x2=4m＜L=10m，故滑上CD初速度为3m/s，
减速运动时间为： 
此时传送运动位移为s=vt2=3m，故△l=x2-s=4-3=1m
（3）物体离开传送带后能到达同一位置，则说明末速度一样都为3m/s，设初速度为v0，位移为L=10m
若v0＞3m/s则做匀减速运动，位移为： 
解得初速度最大值为： 
若v0＜3m/s则做匀加速运动，由（1）分析知初速度最小为0，初速度的范围为0-7m/s，物体离开传送带后能到达同一位置。
