题目内容
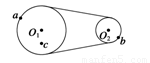
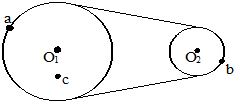 如图所示为一皮带传送装置,a、b分别是两轮边缘上的两点,c处在O1轮上,且有ra=2rb=2rc,则下列关系正确的有( )
如图所示为一皮带传送装置,a、b分别是两轮边缘上的两点,c处在O1轮上,且有ra=2rb=2rc,则下列关系正确的有( )分析:两轮子靠传送带传动,轮子边缘上的点线速度大小相等;同轴转动各点具有相同的角速度;然后根据公式v=ωr和a=
=ω2R分析即可.
| v2 |
| R |
解答:解:A、点a与b点是两轮边缘上的两点,故va=vb,故A正确;
B、点a与点b是两轮的边缘点,故va=vb;,由于a、b的半径之比为2:1,根据公式v=ωr得:?a:?b=1:2,故B错误;
C、点a与点c是同轴传动,角速度相等,半径之比为2:1,故va:vc=2:1,故C错误;
D、va:vc=2:1,va=vb,故vb:vc=2:1;
根据公式a=
,ab:ac=4:1,故D正确;
故选:AD.
B、点a与点b是两轮的边缘点,故va=vb;,由于a、b的半径之比为2:1,根据公式v=ωr得:?a:?b=1:2,故B错误;
C、点a与点c是同轴传动,角速度相等,半径之比为2:1,故va:vc=2:1,故C错误;
D、va:vc=2:1,va=vb,故vb:vc=2:1;
根据公式a=
| v2 |
| r |
故选:AD.
点评:本题关键明确同缘传动边缘点线速度相等,同轴传动角速度相等,然后根据公式v=ωr和a=
=ω2r分析.
| v2 |
| r |

练习册系列答案
相关题目
如图所示为一皮带传送装置,a、b分别是两轮边缘上的两点, c处在O1轮上,且有ra=2rb=2rc,则下列关系正确的有( )
| A.va=vb | B.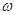 a= a=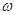 b b |
| C.va=vc | D.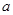 b: b: 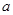 c=4:1 c=4:1 |
 如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示.
如图所示为一皮带传送装置,皮带保持匀速率运动,货物由静止放到传送带上,被传送带向下传送,其运动的v-t图象如图乙所示.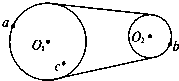 如图所示为一皮带传送装置,a、b分别是两轮边缘上的两点,c处在O1轮上,且有ra=2rb=2rc,则下列关系正确?的有?( )
如图所示为一皮带传送装置,a、b分别是两轮边缘上的两点,c处在O1轮上,且有ra=2rb=2rc,则下列关系正确?的有?( )