题目内容
如图所示，A、B、C、D四图中的小球以及小球所在的左侧斜面完全相同，现从同一高度h处由静止释放小球，使之进入右侧不同的轨道：除去底部一小段圆弧，A图中的轨道是一段斜面，高度大于h；B图中的轨道与A图中轨道相比只是短了一些，且斜面高度小于h；C图中的轨道是一个内径略大于小球直径的管道，其上部为直管，下部为圆弧形，与斜面相连，管的高度大于h；D图中的轨道是个半圆形轨道，其直径等于h.如果不计任何摩擦阻力和拐弯处的能量损失，小球进入右侧轨道后能到达h高度的是
AC
解析试题分析：小球到达最高点的速度可以为零，根据机械能守恒定律得，mgh+0=mgh′+0．则h′=h．故A正确．小球离开轨道做斜抛运动，运动到最高点在水平方向上有速度，即在最高点的速度不为零，根据机械能守恒定律得，mgh+0=mgh′+
mv2．则h′＜h．故B错误． 小球离开轨道做竖直上抛运动，运动到最高点速度为零，根据机械能守恒定律得，mgh+0=mgh′+0．则h′=h．故C正确． 小球在内轨道运动，通过最高点有最小速度，故在最高点的速度不为零，根据机械能守恒定律得，mgh+0=mgh′+mv2．则h′＜h．故D错误．
故选AC．
考点：机械能守恒定律；牛顿第二定律；向心力。
如图所示，小车沿水平面做直线运动，小车内光滑底面上有一物块被压缩的弹簧压向左壁，小车向右加速运动。若小车向右加速度增大，则车左壁受物块的压力N1和车右壁受弹簧的压力N2的大小变化是：
| A．N1不变，N2变大 |
| B．N1变大，N2不变 |
| C．N1、N2都变大 |
| D．N1变大，N2减小 |
一个质量为0.3kg的物体沿水平面做直线运动，如图所示，图线a表示物体受水平拉力时的v—t图象，图线b表示撤去水平拉力后物体继续运动的v—t图象，下列说法中正确的是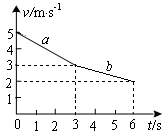 
| A．水平拉力的大小为0.1N，方向与摩擦力方向相同 |
| B．水平拉力对物体做功为1.2J |
| C．撤去拉力后物体还能滑行7.5m |
| D．物体与水平面间的动摩擦因数为0.1 |
如图所示，物块M在静止的传送带上以速度v匀速下滑时，传送带突然启动，方向如图中箭头所示，若传送带的速度大小也为v，则传送带启动后
| A．M静止在传送带上 |
| B．M可能沿传送带向上运动 |
| C．M受到的摩擦力不变 |
| D．M下滑的速度不变 |
如图所示，在竖直平面内有一个半径为R的圆弧轨道。半径OA水平、OB竖直，一个质量为m的小球自A正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力，已知PA=2R，重力加速度为g，则小球 （ ）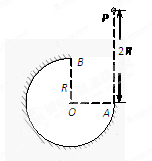
| A．从B点飞出后恰能落到A点 |
| B．从P到B的运动过程中机械能守恒 |
C．从P到B的运动过程中合外力做功 mgR |
| D．从P到B的运动过程中克服摩擦力做功mgR |
在光滑的水平地面上有一木块（视为质点），在水平恒力F的作用下，由静止开始，经过2s时间速度达到10m/s，2s末把外力水平旋转90°大小保持不变，在经过2s到达某一点，则（ ）
A．4s末木块距出发点的距离10 m |
| B．4s末木块距出发点的距离30m |
C．4s末木块的速度大小10 m/s |
| D．4s末木块的速度大小20m/s |
质量为1 kg的物体以某一初速度在水平地面上滑行，由于受到地面摩擦阻力作用，其动能随位移变化的图线如图所示，
，则物体在水平地面上( )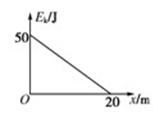
| A．所受合外力大小为5 N |
| B．滑行的总时间为5 s |
| C．滑行的加速度大小为1 m/s2 |
| D．滑行的加速度大小为2.5 m/s2 |