题目内容
1.在光滑水平面上有一比荷$\frac{q}{m}$=1.0×10-7 C/kg的带正电小球,静止在O点,以O点为原点,在水平面内建立坐标系xOy,现突然加一沿x轴正方向、电场强度为2.0×106V/m的匀强电场,小球开始运动. 经过1.0s,所加电场突然变为沿y轴正方向,电场强度大小不变.则小球运动的轨迹和位置坐标正确的是下图中的( )| A. | 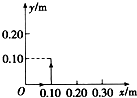 | B. | 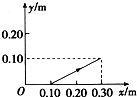 | C. | 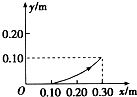 | D. | 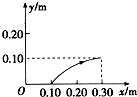 |
分析 由题意可知,带电小球在第1s内沿x轴正方向做匀加速直线运动,第2s、3s内做类平抛运动,根据牛顿第二定律和运动学公式结合求得包括x方向与y方向的分位移,要分别计算出,然后求出合位移,即可求出小球第3s末的位置.
解答 解:第1s内小球沿x轴正方向做初速度为零的匀加速直线运动:
加速度为 a1=$\frac{qE}{m}$=1.0×10-7×2.0×106=0.2m/s2;位移 x1=$\frac{1}{2}$a1${t}_{1}^{2}$=$\frac{1}{2}×0.2×1$m=0.10m
第1s末的速度为 v1=a1t1=0.2m/s
第2s、3s内小球做类平抛运动,轨迹是抛物线,由于电场力沿y轴正方向,所以轨迹向上弯曲.
加速度大小为 a2=a1=$\frac{qE}{m}$=0.2m/s2;
当通过的位移为 x2=0.2m时,用时 t2=$\frac{{x}_{2}}{{v}_{1}}$=$\frac{0.2}{0.2}$s=1s
则 y=$\frac{1}{2}a{t}_{2}^{2}$=$\frac{1}{2}×0.2×{1}^{2}$m=0.1m,故C正确,ABD错误.
故选:C
点评 本题要根据小球的运动情况,运用运动的分解处理类平抛运动.解题的关键是:第2s、3s内做类平抛运动,运用运动的分解法进行研究,要能分别计算出x方向与y方向的位移,从而确定出小球的位置.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 根据图所示的时间坐标轴,下列有关时刻与时间的叙述正确的是( )
根据图所示的时间坐标轴,下列有关时刻与时间的叙述正确的是( )
 根据图所示的时间坐标轴,下列有关时刻与时间的叙述正确的是( )
根据图所示的时间坐标轴,下列有关时刻与时间的叙述正确的是( )| A. | t2表示时刻,称为第2秒末或第3秒初,也可以称为2秒时 | |
| B. | 0~t2表示时间,称为最初2秒内或第2秒内 | |
| C. | t2~t3表示时间,称为第3秒内 | |
| D. | tn-1~tn表示时间,称为第n秒内 |
9.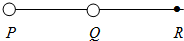 如图2,电荷量为q1和q2的两个点电荷分别位于P点和Q点.已知在P、Q连线上某点R处的电场强度为零,且PQ=RQ.则( )
如图2,电荷量为q1和q2的两个点电荷分别位于P点和Q点.已知在P、Q连线上某点R处的电场强度为零,且PQ=RQ.则( )
 如图2,电荷量为q1和q2的两个点电荷分别位于P点和Q点.已知在P、Q连线上某点R处的电场强度为零,且PQ=RQ.则( )
如图2,电荷量为q1和q2的两个点电荷分别位于P点和Q点.已知在P、Q连线上某点R处的电场强度为零,且PQ=RQ.则( )| A. | q1=2q2 | B. | q1=4q2 | C. | q1=-2q2 | D. | q1=-4q2 |
16. 图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )
图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )
 图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )
图中的平行直线表示一簇垂直于纸面的等势面.一个电量为-5.0×10-8C的点电荷,沿图中曲线从A点移到B点,电场力做的功为( )| A. | -5.0×10-7J | B. | 5.0×10-7J | C. | -3.5×10-7J | D. | 3.5×10-7J |
6.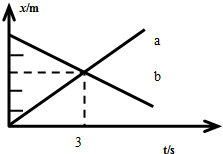 两个物体a、b同时开始沿同一条直线运动.从开始运动起计时,它们的位移图象如图所示.关于这两个物体的运动,下列说法中正确的是( )
两个物体a、b同时开始沿同一条直线运动.从开始运动起计时,它们的位移图象如图所示.关于这两个物体的运动,下列说法中正确的是( )
 两个物体a、b同时开始沿同一条直线运动.从开始运动起计时,它们的位移图象如图所示.关于这两个物体的运动,下列说法中正确的是( )
两个物体a、b同时开始沿同一条直线运动.从开始运动起计时,它们的位移图象如图所示.关于这两个物体的运动,下列说法中正确的是( )| A. | 开始时a的速度较大,加速度较小 | |
| B. | a做匀减速运动,b做匀加速运动 | |
| C. | a、b速度方向相反,速度大小之比是3:2 | |
| D. | 在t=3s时刻a、b速度相等 |
10.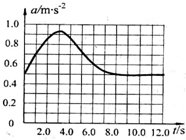 某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示.由图可以得出( )
某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示.由图可以得出( )
 某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示.由图可以得出( )
某研究性学习小组用加速度传感器探究物体从静止开始做直线运动的规律,得到了质量为1.0kg的物体运动的加速度随时间变化的关系图线,如图所示.由图可以得出( )| A. | 从t=4.0s到t=6.0s的时间内物体做匀减速直线运动 | |
| B. | 物体在t=10.0s时的速度大小约为6.8m/s | |
| C. | 从t=10.0s到t=12.0s的时间内合外力对物体做的功约为0.5J | |
| D. | 从t=2.0s到t=6.0s的时间内物体所受合外力先减小后增大 |
11.在物理学发展的过程中,有许多伟大的科学家做出了贡献.关于科学家和他们的贡献,下列说法正确的是( )
| A. | 法拉第提出了著名的分子电流假说 | |
| B. | 奥斯特根据小磁针在通电导线周围的偏转而发现了电流的磁效应 | |
| C. | 安培根据扭秤实验得到了点电荷间的静电力的表达式 | |
| D. | 库伦首先提出了电场的概念 |
 在电场中一条电场线上有A、B两点,如图所示.若将一负电荷q=2.0×10-7C,从A点移至B点,电荷克服电场力做功4.0×10-4J.试求:
在电场中一条电场线上有A、B两点,如图所示.若将一负电荷q=2.0×10-7C,从A点移至B点,电荷克服电场力做功4.0×10-4J.试求: