题目内容
12.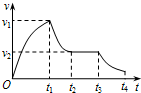 2012年10月15日著名极限运动员鲍姆加特纳从3.9万米的高空跳下,并成功着陆.假设他沿竖直方向下落,其v-t图象如图所示,则下列说法中正确的是( )
2012年10月15日著名极限运动员鲍姆加特纳从3.9万米的高空跳下,并成功着陆.假设他沿竖直方向下落,其v-t图象如图所示,则下列说法中正确的是( )| A. | 0~t1时间内运动员及其装备机械能守恒 | |
| B. | t1~t2时间内运动员处于超重状态 | |
| C. | t1~t2时间内运动员的平均速度$\overline v<\frac{{{v_1}+{v_2}}}{2}$ | |
| D. | t2~t4时间内重力对运动员所做的功等于他克服阻力所做的功 |
分析 速度时间图象的斜率等于加速度,根据斜率分析加速度大小如何变化,判断运动员的运动情况.将运动员的运动与匀变速运动进行比较,分析其平均速度.根据功能关系分析重力做功与克服阻力做功的关系.
解答 解:A、0-t1内图线的斜率在减小,说明运动员做加速度逐渐减小的加速运动,加速度方向向下,所以运动员及其装备一定受到阻力作用,机械能不守恒,故A错误;
B、t1~t2时间内由于图象的斜率在减小,斜率为负值,说明加速度方向向上,根据牛顿运动定律得知运动员处于超重状态,故B正确;
C、t1~t2时间内,若运动员做匀减速运动,平均速度等于$\frac{{v}_{1}{+v}_{2}}{2}$,而根据“面积”表示位移得知,此过程的位移小于匀减速运动的位移,所以此过程的平均速度$\overline v<\frac{{{v_1}+{v_2}}}{2}$,故C正确;
D、t2~t4时间内重力做正功,阻力做负功,由于动能减小,根据动能定理得知,外力对运动员做的总功为负值,说明重力对运动员所做的功小于他克服阻力所做的功,故D错误.
故选:BC.
点评 本题考查理解速度问题的能力.关键根据图线的斜率等于加速度,来分析运动员的运动情况.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.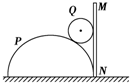 半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )
 半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )
半圆柱体P放在粗糙的水平地面上,其右端有一固定放置的竖直挡板MN.在半圆柱体P和MN之间放有一个光滑均匀的小圆柱体Q,整个装置处于平衡状态,如图所示是这个装置的截面图.现使MN保持竖直并且缓慢地向右平移,在Q滑落到地面之前,发现P始终保持静止,则在此过程中,下列说法正确的是( )| A. | MN对Q的弹力逐渐减小 | B. | P对Q的弹力逐渐增大 | ||
| C. | 地面对P的摩擦力逐渐减小 | D. | Q所受的合力逐渐增大 |
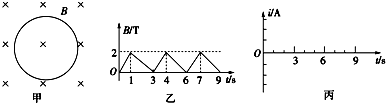

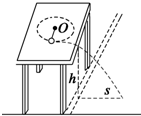 如图所示,一根长为0.1m的细线,一端系着一个质量是0.18kg的小球,拉住线的另一端,使球在光滑的水平桌面上做匀速圆周运动,当小球的转到如图位置时,细线断裂,这时测得线的拉力为45N,并在桌子上匀速滚动一段距离后,垂直桌子边缘水平飞出.求:
如图所示,一根长为0.1m的细线,一端系着一个质量是0.18kg的小球,拉住线的另一端,使球在光滑的水平桌面上做匀速圆周运动,当小球的转到如图位置时,细线断裂,这时测得线的拉力为45N,并在桌子上匀速滚动一段距离后,垂直桌子边缘水平飞出.求: 一列横波沿x轴方向传播,在t1=0时刻的波形图如图中实线所示,在t2=1s时刻的波形如图中的虚线所示,求:
一列横波沿x轴方向传播,在t1=0时刻的波形图如图中实线所示,在t2=1s时刻的波形如图中的虚线所示,求: