题目内容
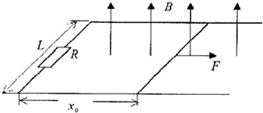 如图所示,水平光滑平行导轨间距L=lm,左端接有阻值R=1.5Ω的定值电阻,在距左端x0=2m处垂直导轨放置一根质量m=1kg、电阻r=0.5Ω的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中.
如图所示,水平光滑平行导轨间距L=lm,左端接有阻值R=1.5Ω的定值电阻,在距左端x0=2m处垂直导轨放置一根质量m=1kg、电阻r=0.5Ω的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中.(1)若磁场的磁感应强度B随时间t变化的关系为B=0.5+0.1t(式中B的单位为T,t的单位为s),为使导体棒保持静止,求作用在导体棒上的水平拉力F随时间t变化的规律;
(2)若磁场的磁感应强度B=0.5T恒定,t=0时导体棒在水平拉力F的作用下从静止开始向右做匀加速直线运动,已知t=4s时F=3N,求此时导体棒两端的电势差.
分析:(1)导体棒切割磁感线运动产生感应电动势和感应电流,根据安培力表达式,结合安培力与电场力相平衡,即可求解;
(2)导体棒由静止在外力作用下,加速度运动,由受力分析,根据牛顿第二定律,结合感应电动势的大小及运动学公式,即可求出导体棒两端的电势差.
(2)导体棒由静止在外力作用下,加速度运动,由受力分析,根据牛顿第二定律,结合感应电动势的大小及运动学公式,即可求出导体棒两端的电势差.
解答:解:(1)由法拉第电磁感应定律:E=
=
Lx0=0.1×1×2V=0.2V①
解得,F=BIL=
=(5+t)×10-2(N)②
(2)由牛顿第二定律:F-BIL=ma③
I=
④
感应电动势:E=BLv⑤
速度为:v=at⑥
联立③④⑤⑥得:F=
at+ma⑦
代入数据解得:a=2m/s2,v=8m/s,E=4V,I=2A
电势差:U=IR=2×1.5V=3V
答:(1)作用在导体棒上的水平拉力F随时间t变化的规律为F=(5+t)×10-2N;
(2)此时导体棒两端的电势差3V.
| △Φ |
| △t |
| △B |
| △t |
解得,F=BIL=
| BLE |
| R+r |
(2)由牛顿第二定律:F-BIL=ma③
I=
| E |
| R+r |
感应电动势:E=BLv⑤
速度为:v=at⑥
联立③④⑤⑥得:F=
| B2L2 |
| R+r |
代入数据解得:a=2m/s2,v=8m/s,E=4V,I=2A
电势差:U=IR=2×1.5V=3V
答:(1)作用在导体棒上的水平拉力F随时间t变化的规律为F=(5+t)×10-2N;
(2)此时导体棒两端的电势差3V.
点评:解决本题的关键掌握导体切割产生的感应电动势E=BLv,以及感生产生的电动势E=n
.理解牛顿第二定律与运动学公式综合应用,注意求电势差时,电阻不能代错.
| △? |
| △t |

练习册系列答案
相关题目
 如图所示,水平轻弹簧左端固定在竖直墙上,右端被一用轻质细线拴住的质量为m的光滑小球压缩(小球与弹簧未拴接).小球静止时离地高度为h.若将细线烧断,则(取重力加速度为g,空气阻力不计)( )
如图所示,水平轻弹簧左端固定在竖直墙上,右端被一用轻质细线拴住的质量为m的光滑小球压缩(小球与弹簧未拴接).小球静止时离地高度为h.若将细线烧断,则(取重力加速度为g,空气阻力不计)( )| A、小球立即做平抛运动 | ||
| B、细线烧断瞬间小球的加速度为重力加速度g | ||
| C、小球脱离弹簧后做匀变速运动 | ||
D、小球落地时重力瞬时功率等于mg
|
 如图所示,在光滑水平桌面上,平放一根两端封闭的内壁光滑的真空玻璃管,管长为L,管中一端放有一个质量为m,电荷量为+q的小球,此空间存在着垂直桌面向下的磁场,磁感应强度为B.现在给玻璃管施一平行桌面垂直管子的力,维持管子在桌面上以速度v作匀速平动,小球从管的底端开始向另一端运动,下述判断中正确的是( )
如图所示,在光滑水平桌面上,平放一根两端封闭的内壁光滑的真空玻璃管,管长为L,管中一端放有一个质量为m,电荷量为+q的小球,此空间存在着垂直桌面向下的磁场,磁感应强度为B.现在给玻璃管施一平行桌面垂直管子的力,维持管子在桌面上以速度v作匀速平动,小球从管的底端开始向另一端运动,下述判断中正确的是( )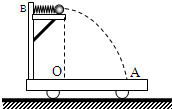 如图所示,水平光滑的桌面上放一质量为M的玩具小车,在小车的光滑的平台上有一质量可忽略的弹簧,弹簧的一端固定在平台上的B点,另一端接触质量为m的小球.若小车固定在桌面上,压缩弹簧,克服弹簧的弹力做功W时,将小球用细线拴住,然后烧断细线,小球被弹出,落在车上的A点.若小车不固定,压缩弹簧后用细线拴住小球,当小车和小球都静止时,烧断细线,将小球弹出.问:要想使小球也落到A点.压缩弹簧时,需克服弹簧弹力做多少功?(设弹簧压缩量远小于OA距离)
如图所示,水平光滑的桌面上放一质量为M的玩具小车,在小车的光滑的平台上有一质量可忽略的弹簧,弹簧的一端固定在平台上的B点,另一端接触质量为m的小球.若小车固定在桌面上,压缩弹簧,克服弹簧的弹力做功W时,将小球用细线拴住,然后烧断细线,小球被弹出,落在车上的A点.若小车不固定,压缩弹簧后用细线拴住小球,当小车和小球都静止时,烧断细线,将小球弹出.问:要想使小球也落到A点.压缩弹簧时,需克服弹簧弹力做多少功?(设弹簧压缩量远小于OA距离)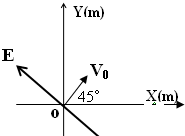 如图所示,在光滑水平绝缘平面上,水平匀强电场方向与X轴间成135°角,电场强度E=1×103N/c,某带电小球电量为q=-2×10-6c,质量m=1×10-3kg,以初速度V0=2m/s从坐标轴原点出发,在XOY平面内运动,V0与水平匀强电场垂直,
如图所示,在光滑水平绝缘平面上,水平匀强电场方向与X轴间成135°角,电场强度E=1×103N/c,某带电小球电量为q=-2×10-6c,质量m=1×10-3kg,以初速度V0=2m/s从坐标轴原点出发,在XOY平面内运动,V0与水平匀强电场垂直,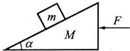 如图所示,在光滑水平而上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用平力F(未知)推斜劈,恰使物体m与斜劈间无相对滑动,则m的加速度大小为
如图所示,在光滑水平而上有一质量为M的斜劈,其斜面倾角为α,一质量为m的物体放在其光滑斜面上,现用平力F(未知)推斜劈,恰使物体m与斜劈间无相对滑动,则m的加速度大小为