Question

【题目】如图，大猴想借助一根青藤救回对岸的小猴。已知：大猴质量M=20kg，小猴质量m=5kg，青藤长度L1=5m，等高的两岸间的水平距离L2=8m，重力加速度g=10m/s2。青藤悬点O离两岸的水平距离相等，猴子视为质点，忽略空气阻力及青藤质量。若青藤能承受的最大拉力为400N，请通过计算分析说明大猴能否顺利摆到对岸并将小猴安全救回。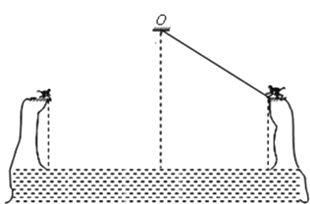

Answer 1

【答案】解：根据几何关系可得：
对大猴研究可得：

②③联立得
以两个猴子整体为研究对象，从岸上到最低点的过程，根据机械能守恒定律得


④⑤联立得
因360N<400N，故大猴可以安全摆到对岸
因450N>400N，故大猴不能将小猴安全抱回
【解析】考查了动能定理，圆周运动；解决本题的关键要正确分析受力情况，确定最低点向心力的来源，运用机械能守恒和牛顿第二定律结合研究，以两个猴子整体为研究对象，根据机械能守恒定律求出猴子通过最低点时的速度，再由向心力公式求出青藤的拉力，即可判断
【考点精析】根据题目的已知条件，利用动能定理的综合应用的相关知识可以得到问题的答案，需要掌握应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷．