题目内容
如图所示,平行金属导轨与水平面间夹角均为θ= 370 ,导轨间距为 lm ,电阻不计,导轨足够长。两根金属棒 ab 和 a' b'的质量都是0.2kg,电阻都是 1Ω ,与导轨垂直放置且接触良好,金属棒a' b'和导轨之间的动摩擦因数为0.5 ,设金属棒a' b'受到的最大静摩擦力等于滑动摩擦力。金属棒ab和导轨无摩擦,导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场,导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场,磁感应强度 B 的大小相同。用外力让a' b'固定不动,将金属棒ab 由静止释放,当 ab 下滑速度达到稳定时,整个回路消耗的电功率为 18W。求:
(1)ab 棒达到的最大速度;
(2)ab棒下落了 30m 高度时,其下滑速度已经达到稳定,此过程中回路电流产生的焦耳热 Q ;
(3)在ab棒下滑过程中某时刻将 a' b'固定解除,为确保a' b'始终保持静止,则a' b'固定解除时ab棒的速度大小满足什么条件? ( g ="10m" / s2,sin370 ="0.6" ,cos370 ="0.8" )
(1)ab 棒达到的最大速度;
(2)ab棒下落了 30m 高度时,其下滑速度已经达到稳定,此过程中回路电流产生的焦耳热 Q ;
(3)在ab棒下滑过程中某时刻将 a' b'固定解除,为确保a' b'始终保持静止,则a' b'固定解除时ab棒的速度大小满足什么条件? ( g ="10m" / s2,sin370 ="0.6" ,cos370 ="0.8" )

(1) (2)
(2)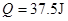 (3)10m/s≤v≤15m/s
(3)10m/s≤v≤15m/s
 (2)
(2)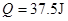 (3)10m/s≤v≤15m/s
(3)10m/s≤v≤15m/s(1)ab下滑速度达到稳定时,加速度为0,速度达到最大,
由电功率定义可知: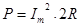 解得:
解得:
对ab由平衡条件得:
解得: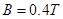 (2分)
(2分)
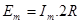 ,解得
,解得
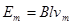 ,解得
,解得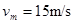 (2分)
(2分)
(或由能量守恒得: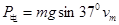 解得:
解得: (2分))
(2分))
(2)根据动能定理得: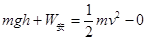
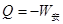
解得: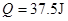 (4分)
(4分)
(或由能量守恒得: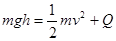 解得:
解得: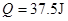 (4分))
(4分))
(3)对a' b'棒
垂直于导轨平面方向: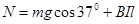 (1分)
(1分)
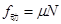 (1分)
(1分)
平行于导轨平面方向: (`1分)
(`1分)
可得: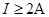
对ab棒: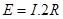
 解得
解得 (1分)
(1分)
a' b'固定解除时ab棒的速度满足:10m/s≤v≤15m/s
本题考查的是电磁感应定律和力学综合的问题,利用受力分析或能量守恒和电磁感应定律可以得出棒达到的最大速度;利用动能定理可得到安培力做的功即焦耳热;通过受力关系,利用电磁感应定律可解得最后结果;
由电功率定义可知:
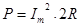 解得:
解得:
对ab由平衡条件得:

解得:
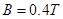 (2分)
(2分)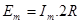 ,解得
,解得
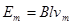 ,解得
,解得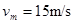 (2分)
(2分)(或由能量守恒得:
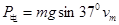 解得:
解得: (2分))
(2分))(2)根据动能定理得:
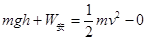
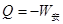
解得:
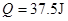 (4分)
(4分)(或由能量守恒得:
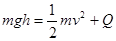 解得:
解得: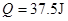 (4分))
(4分))(3)对a' b'棒
垂直于导轨平面方向:
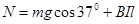 (1分)
(1分)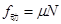 (1分)
(1分)平行于导轨平面方向:
 (`1分)
(`1分)可得:
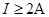
对ab棒:
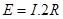
 解得
解得 (1分)
(1分)a' b'固定解除时ab棒的速度满足:10m/s≤v≤15m/s
本题考查的是电磁感应定律和力学综合的问题,利用受力分析或能量守恒和电磁感应定律可以得出棒达到的最大速度;利用动能定理可得到安培力做的功即焦耳热;通过受力关系,利用电磁感应定律可解得最后结果;

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目



 >
> ,20V
,20V >
>


 (
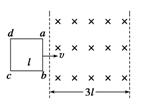
( 为常量).一边长为
为常量).一边长为 的线框,其电阻为R,线框有一半面积处于磁场区域中.则线框中感应电流的
的线框,其电阻为R,线框有一半面积处于磁场区域中.则线框中感应电流的
