Question

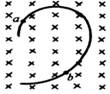
如图所示，放置在平面中第二象限内P点的粒子放射源连续放出质量均为m、电量为-q的一簇粒子，已知入射粒子以同一速度v朝x轴以上向不同方向散开，垂直纸面的匀强磁场B将这些粒子聚焦于R点(磁场区域大致如图所示)，其中已知PR=2a，离子的轨迹关于y轴对称的。试确定磁场区域的边界函数方程。不计粒子重力及相互间的作用。

Answer 1

    

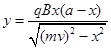
试题分析：在磁场B中，粒子受洛仑兹力作用作半径为R的圆周运动：

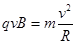 即：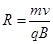
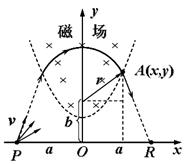
设半径为R的圆轨道上运动的粒子，在点A (x，y)离开磁场，沿切线飞向R点。
由相似三角形得到：   
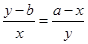
同时，A作为轨迹圆上的点，应满足方程：
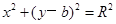
消去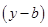，得到满足条件的A点的集合，
因此，表示磁场边界的函数方程为： 
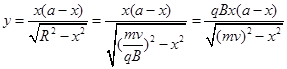
即所求磁场边界方程为：  
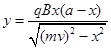
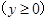
点评：本题由于结合较多的数学知识，特别是圆的性质，故此类题型重点在于熟练把握圆的性质；可以先大致画出圆的轨迹，根据偏转方向等确定出圆心和半径，再利用几何知识求出结果。