题目内容
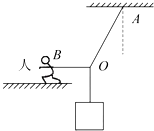
【题目】如图所示，长为2L的轻杆上端固定一质量为m的小球，下端用光滑铰链连接于地面上的O点，杆可绕O点在竖直平面内自由转动，定滑轮固定于地面上方L处，电动机由跨过定滑轮且不可伸长的绳子与杆的中点相连，启动电动机，杆从虚线位置绕O点逆时针倒向地面，假设整个倒下去的过程中，杆做匀速转动，则在此过程中（ ）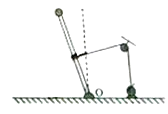
A.小球重力做功为2mgL
B.绳子拉力做功大于2mgL
C.重力做功功率逐渐增大
D.绳子拉力做功功率先增大后减小
【答案】A,C
【解析】解：A、小球重力做功为W=mg2L=2mgL，故A正确；
B、在整个过程中，根据动能定理可得W﹣mg 
，解得W=2mgL，故B错误；
C、根据P=Fvcosθ可知，P=mgvcosθ，在下落过程中，θ逐渐减小，故重力做功功率逐渐增大，故C正确；
D、在整个过程中，重力的功率和绳子的功率相同，故绳子的功率逐渐增大，故D错误；
故选：AC
【考点精析】认真审题，首先需要了解动能定理的综合应用(应用动能定理只考虑初、末状态，没有守恒条件的限制，也不受力的性质和物理过程的变化的影响.所以，凡涉及力和位移，而不涉及力的作用时间的动力学问题，都可以用动能定理分析和解答，而且一般都比用牛顿运动定律和机械能守恒定律简捷)．
练习册系列答案
相关题目
