题目内容
3. 在粗糙的水平面上有两个静止的物体A、B,它们的质量均为m=2kg.A与水平面间的动摩擦因数为μ1=0.4,B与水平面间的动摩擦因数μ2=0.2.在水平恒力F=20N的作用下从静止开始向右做匀加速直线运动,F作用了t=2s然后撤掉.g=10m/s2.求:
在粗糙的水平面上有两个静止的物体A、B,它们的质量均为m=2kg.A与水平面间的动摩擦因数为μ1=0.4,B与水平面间的动摩擦因数μ2=0.2.在水平恒力F=20N的作用下从静止开始向右做匀加速直线运动,F作用了t=2s然后撤掉.g=10m/s2.求:(1)在水平恒力F的作用下A、B间的作用力大小
(2)撤掉F后1.5s时A、B间的距离L.
分析 (1)先整体求得AB的共同加速度,再隔离分析求AB间的作用力;
(2)撤去外力F后,AB都在摩擦力作用下做匀减速运动,AB间的距离即为它们匀减速运动时的位移差
解答 解:(1)以AB整体为研究对象进行受力分析,由牛顿第二定律得:
F-μ1mg-μ2mg=2ma
可得物体整体运动的加速度为:
a=$\frac{F-{μ}_{1}mg-{μ}_{2}mg}{2m}=\frac{20-0.4×2×10-0.2×2×10}{2×2}$m/s2=2m/s2
对A受力分析可知A在水平方向受推力F和B对A的作用力N,以及地面摩擦力作用,根据牛顿第二定律有:
F-μ1mg-N=ma
可得B对A的作用力为:
N=F-μ1mg-ma=20-0.4×2×10-2×2N=8N,方向由B指向A(或向左)
(2)根据速度时间关系知,撤去外力F后,AB整体的速度为:v=at=2×2m/s=4m/s
撤去F后:A的加速度大小为:aA=μ1g=0.4×10m/s2=4m/s2
A减速到0所需时间为:t$′=\frac{v}{{a}_{A}}=\frac{4}{4}s=1s<1.5s$
A的位移大小为:${x}_{A}=\frac{{v}^{2}}{2{a}_{A}}=\frac{{4}^{2}}{2×4}m=2m$
撤去力F后,B的加速度大小为:aB=μ2g=0.2×10m/s2=2m/s2
1.5s时B的速度为:v′′=v-aBt=4-2×1.5m/s=1m/s
B的位移大小为:${x}_{B}=vt-\frac{1}{2}{a}_{B}{t}^{2}=4×1.5-\frac{1}{2}×2×1.{5}^{2}$m=3.75m
所以A、B都静止时它们之间的距离为:L=xB-xA=4-2m=1.75m
答:(1)A、B一起运动的过程中B对A的作用力为9N,方向水平向左;
(2)A、B都静止时它们之间的距离L为1.75m
点评 对于连接体问题要善于运用整体法和隔离法抓住整体和隔离体加速度相等进行求解,正确的受力分析求加速度是解题的突破口

 名校课堂系列答案
名校课堂系列答案| A. | 晶体和非晶体的区别在于是否具有各向异性 | |
| B. | 单晶体具有一定的熔点,多晶体没有一定的熔点 | |
| C. | 某些昆虫能飘浮在水面上是因为其所受重力与浮力平衡 | |
| D. | 液晶像液体具有流动性,又像晶体,分子在特定方向排列比较整齐,具有各向异性 |
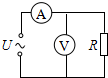
| A. | 14.1 A,200 V | B. | 2 A,200 V | C. | 14.1 A,141 V | D. | 2 A,141 V |
 如图所示,一块通电的铜板放在磁场中,板面垂直磁场,板内通有如图方向的电流,a、b是铜板左、右边缘的两点,则( )
如图所示,一块通电的铜板放在磁场中,板面垂直磁场,板内通有如图方向的电流,a、b是铜板左、右边缘的两点,则( )| A. | 电势φa>φb | |
| B. | 电势φb>φ a | |
| C. | 电势φb=φa | |
| D. | 其他条件不变,将铜板改为NaCl水溶液时,电势结果仍然一样 |
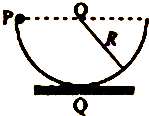 一半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的压力大小为2mg,重力加速度大小为g,正确的有( )
一半径为R的半圆形轨道竖直固定放置,轨道两端等高.质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的压力大小为2mg,重力加速度大小为g,正确的有( )| A. | 质点在Q点速度大小为$\sqrt{2gR}$ | |
| B. | 质点在Q点速度大小为$\sqrt{gR}$ | |
| C. | 质点自P滑到Q的过程中,克服摩擦力所做的功为$\frac{mgR}{2}$ | |
| D. | 质点自P滑到Q的过程中,克服摩擦力所做的功为$\frac{mgR}{4}$ |
| A. | 由公式E=$\frac{F}{q}$知,电场中某点的场强E与电场力F成正比,与电荷的电荷量q成反比 | |
| B. | 由公式E=$\frac{F}{q}$知,电场中某点的电荷所受电场力F与该电荷的电量q成正比 | |
| C. | 在公式E=k$\frac{Q}{{r}^{2}}$中,E是电荷Q产生的电场的场强 | |
| D. | E=k$\frac{Q}{{r}^{2}}$只能用于点电荷产生的电场,而E=$\frac{F}{q}$可用于任何电场 |
 将一质量为mq=0.1kg、长为0.5m的长木板放在光滑的水平桌面上,且长木板以vq=1m/s的速度水平向左运动,今有一可视为质点的质量为mp=0.2kg的滑块由长木板的左端以vp=3m/s的水平向右的速度滑上长木板,最终从长木板的左端离开,已知滑块与长木板间的动摩擦因数为μ=0.5,重力加速度取g=10m/s2,则整个过程中滑块对长模板的冲量大小为多少?
将一质量为mq=0.1kg、长为0.5m的长木板放在光滑的水平桌面上,且长木板以vq=1m/s的速度水平向左运动,今有一可视为质点的质量为mp=0.2kg的滑块由长木板的左端以vp=3m/s的水平向右的速度滑上长木板,最终从长木板的左端离开,已知滑块与长木板间的动摩擦因数为μ=0.5,重力加速度取g=10m/s2,则整个过程中滑块对长模板的冲量大小为多少? 如图所示,竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R=2Ω的电阻,N板上有一小孔Q,在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T.有一质量M=0.2kg、电阻r=1Ω的金属棒搭在MN之间并与MN良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点静止释放一个比荷$\frac{q}{m}$=1×104C/kg的正离子,经电场加速后,以v=200m/s的速度从Q点垂直于N板边界射入右侧区域.不计离子重力,忽略电流产生的磁场,取g=10m/s2.求:
如图所示,竖直平面内放着两根间距L=1m、电阻不计的足够长平行金属板M、N,两板间接一阻值R=2Ω的电阻,N板上有一小孔Q,在金属板M、N及CD上方有垂直纸面向里的磁感应强度B0=1T的有界匀强磁场,N板右侧区域KL上、下部分分别充满方向垂直纸面向外和向里的匀强磁场,磁感应强度大小分别为B1=3T和B2=2T.有一质量M=0.2kg、电阻r=1Ω的金属棒搭在MN之间并与MN良好接触,用输出功率恒定的电动机拉着金属棒竖直向上运动,当金属棒达最大速度时,在与Q等高并靠近M板的P点静止释放一个比荷$\frac{q}{m}$=1×104C/kg的正离子,经电场加速后,以v=200m/s的速度从Q点垂直于N板边界射入右侧区域.不计离子重力,忽略电流产生的磁场,取g=10m/s2.求: