题目内容
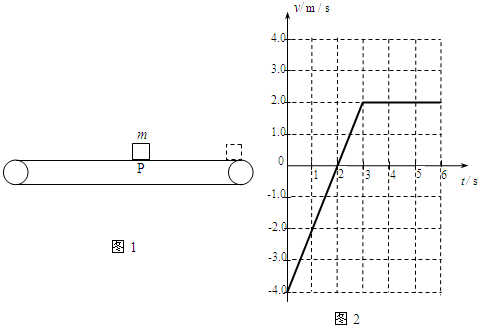
如图1所示,一质量为m=2.0kg的小物块从右侧向左滑上水平传送带.当滑至P点时开始计时,小物块在0-6s内相对地面的v-t图象如图2所示,已知传送带的速度恒定不变,g取10m/s2.
(1)指出传送带速度v的方向及大小,并计算物块与传送带间的动摩擦因数μ.
(2)计算小物块在0-6s内在传送带上相对传送带滑过的路程
(1)指出传送带速度v的方向及大小,并计算物块与传送带间的动摩擦因数μ.
(2)计算小物块在0-6s内在传送带上相对传送带滑过的路程

分析:(1)从v-t图象看出,物块最后随传送带一起向右做匀速运动速度为v=2.0 m/s.
所以,传送带的速度方向向右,其速度为v0=2.0 m/s.
计算物块与传送带之间的摩擦因数,首先从图象中找出物体仅在摩擦力作用下运动时加速度,后由牛顿第二定律摩擦力即可求出 μ.
(2)求物体与传送带之间相对的路程,应该分两段来讨论,第一段物体与传送带向不同的方向运动,相对路程为他们相对地面路程的和;第二段物体与传送带同向运动,相对路程为他们相对地面路程的差.
所以,传送带的速度方向向右,其速度为v0=2.0 m/s.
计算物块与传送带之间的摩擦因数,首先从图象中找出物体仅在摩擦力作用下运动时加速度,后由牛顿第二定律摩擦力即可求出 μ.
(2)求物体与传送带之间相对的路程,应该分两段来讨论,第一段物体与传送带向不同的方向运动,相对路程为他们相对地面路程的和;第二段物体与传送带同向运动,相对路程为他们相对地面路程的差.
解答:解:(1)从v-t图象看出,小物块从右侧向左滑上水平传送带,先向左减速到v=0,然后向右加速到v=2.0 m/s,
以后随传送带一起做匀速运动,所以,传送带的速度方向向右,其速度v0=2.0 m/s.
由速度图象可得,物块在滑动摩擦力的作用下做匀变速运动的加速度为a,
a=
=
m/s2=2.0m/s2
由牛顿第二定律得,滑动摩擦力Ff=μMg=Ma
物块与传送带间的动摩擦因数 μ=
=
=0.2
(2)由速度图象可知,传送带与物块存在摩擦力的时间只有3秒,
0~2s内:s物1=
at12=
×2.0×22m=4m(向左) s带1=v0t1=2.0×2m=4m(向右)
2~3s内:s物2=
at22=
×2.0×12m=1m(向右) s带2=v0t2=2.0×1m=2m(向右)
所以,物块与传送带之间的相对位移△S相=(4m+4m)+(2m-1m)=9m
答:(1)传送带的速度方向向右,其速度为2.0 m/s,物块与传送带间的动摩擦因数为0.2.
(2)小物块在0-6s内在传送带上相对传送带滑过的路程为9m.
以后随传送带一起做匀速运动,所以,传送带的速度方向向右,其速度v0=2.0 m/s.
由速度图象可得,物块在滑动摩擦力的作用下做匀变速运动的加速度为a,
a=
| △v |
| △t |
| 4 |
| 2 |
由牛顿第二定律得,滑动摩擦力Ff=μMg=Ma
物块与传送带间的动摩擦因数 μ=
| a |
| g |
| 2.0 |
| 10 |
(2)由速度图象可知,传送带与物块存在摩擦力的时间只有3秒,
0~2s内:s物1=
| 1 |
| 2 |
| 1 |
| 2 |
2~3s内:s物2=
| 1 |
| 2 |
| 1 |
| 2 |
所以,物块与传送带之间的相对位移△S相=(4m+4m)+(2m-1m)=9m
答:(1)传送带的速度方向向右,其速度为2.0 m/s,物块与传送带间的动摩擦因数为0.2.
(2)小物块在0-6s内在传送带上相对传送带滑过的路程为9m.
点评:本题借助传送带模型考查了匀变速直线运动规律,摩擦因数,牛顿第二定律等知识点,综合性很强,是一道中档题.解题的关键是正确认识匀变速直线运动的v-t图象.

练习册系列答案
相关题目

 (2013?重庆二模)如图1所示,一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下,已知滑块与斜面间的动摩擦因数μ和滑块到斜面顶端的距离x的关系如图2所示.斜面倾角为37°,长为L.有一半径R=
(2013?重庆二模)如图1所示,一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下,已知滑块与斜面间的动摩擦因数μ和滑块到斜面顶端的距离x的关系如图2所示.斜面倾角为37°,长为L.有一半径R=

