题目内容
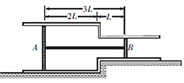
【题目】如图所示，上端带卡环的绝热圆柱形汽缸竖直放置在水平地面上，汽缸内部被质量均为m的活塞A和活塞B分成高度相等的三个部分，下边两部分封闭有理想气体P和Q，活塞A导热性能良好，活塞B绝热。两活塞均与汽缸接触良好，活塞厚度不计，忽略一切摩擦。汽缸下面有加热装置，初始状态温度均为T0，气缸的截面积为S，外界大气压强大小为
且保持不变，现对气体Q缓慢加热。求：
①当活塞A恰好到达汽缸上端卡口时，气体Q的温度T1；
②活塞A恰接触汽缸上端卡口后，继续给气体Q加热，当气体P体积减为原来一半时，气体Q的温度T2。
【答案】(1) 
(2) 
【解析】①设P、Q初始体积均为V0，在活塞A接触卡扣之前，两部分气体均等压变化，则由盖—吕萨克定律
，解得：
；
②当活塞A恰接触汽缸上端卡口后，P气体做等温变化，由玻意耳定律
解得
；
此时Q气体的压强为
；
当P气体体积变为原来一半时，Q气体的体积为
，此过程对Q气体由理想气体状态方程：
，解得
；
练习册系列答案
相关题目
