题目内容
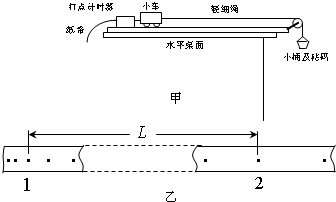
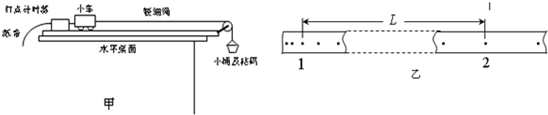
某学习小组采用如图甲所示的实验装置验证动能定理,小车运动过程中所受的阻力Ff已知,实验中,在小桶中加入适当砝码使小车做匀加速运动,打点计时器打出的纸带如图乙所示,通过正确的方法测出纸带上1、2两点的速度为v1、v2,1、2两点间的距离为L,小车的质量为mo及小桶和砝码的总质量m后,某同学按如下思路验证动能定理:以小车为研究对象,它的合外力的功为W合﹦mgL-FfL,动能增加量为△Ek﹦
m0(
-
),比较两者的大小即可验证结论.
(1)实验中用小桶和砝码的总重力mg的大小作为小车所受拉力F的大小,这样做的前提条件是 .
(2)在满足上述(1)的条件下经过多次实验,发现W合仍然总是稍大于△Ek,请你提出一种消除上述误差的方法 ,这种方法验证动能定理的表达式为: .
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |

(1)实验中用小桶和砝码的总重力mg的大小作为小车所受拉力F的大小,这样做的前提条件是
(2)在满足上述(1)的条件下经过多次实验,发现W合仍然总是稍大于△Ek,请你提出一种消除上述误差的方法
分析:(1)用小桶和砝码的总重力mg的大小作为小车所受拉力F的大小,应满足使小桶和砝码的总质量m远小于小车的质量m0.
(2)W合总是稍大于△Ek,消除上述误差的方法之一是以小车、小桶及砝码组成的系统为研究对象.
(2)W合总是稍大于△Ek,消除上述误差的方法之一是以小车、小桶及砝码组成的系统为研究对象.
解答:解:(1)对小桶和钩码来说,根据牛顿第二定律:mg-F=ma,若F≈mg,a必须很小,必须要满足小桶和钩码的质量m远小于小车的总质量mo.
(2)W合总是稍大于△Ek,消除这种误差的方法之一是以小车、小桶及砝码组成的系统为研究对象,系统的合外力做功等于重力与阻力做功的代数和,为W合﹦mgL-FfL,这种方法验证动能定理的表达式为:
mgL-FfL=
(m+m0)(
-
)
故答案为:
(1)小桶和钩码的质量m远小于小车的总质量mo.
(2)以小车、小桶及砝码组成的系统为研究对象,mgL-FfL=
(m+m0)(
-
).
(2)W合总是稍大于△Ek,消除这种误差的方法之一是以小车、小桶及砝码组成的系统为研究对象,系统的合外力做功等于重力与阻力做功的代数和,为W合﹦mgL-FfL,这种方法验证动能定理的表达式为:
mgL-FfL=
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
故答案为:
(1)小桶和钩码的质量m远小于小车的总质量mo.
(2)以小车、小桶及砝码组成的系统为研究对象,mgL-FfL=
| 1 |
| 2 |
| v | 2 2 |
| v | 2 1 |
点评:解决本题的关键掌握实验条件的控制,知道实验的原理以及知道实验误差的来源,能根据实验原理确定减小误差的有效方法.

练习册系列答案
相关题目