题目内容
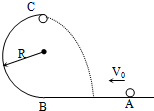 如图所示,AB为一长为L的水平轨道,质量为m的小球从A点以初速度v0做匀速直线运动,然后冲上竖直平面内半径为R的光滑半圆轨道,到达最高点C后抛出,最后落回地面,如图所示,试求:
如图所示,AB为一长为L的水平轨道,质量为m的小球从A点以初速度v0做匀速直线运动,然后冲上竖直平面内半径为R的光滑半圆轨道,到达最高点C后抛出,最后落回地面,如图所示,试求:(1)小球在C点对半圆轨道的压力?
(2)小球落到地面上时距离B点的距离?(g取10m/s2)
分析:(1)从A到C的过程中,根据动能定理列式求出到达C点的速度,再根据向心力公式列式求解小球在C点对半圆轨道的压力;
(2)小球从C点抛出后做平抛运动,根据平抛运动的基本公式即可求解.
(2)小球从C点抛出后做平抛运动,根据平抛运动的基本公式即可求解.
解答:解:(1)从A到C的过程中,根据动能定理得:
mvC2-
mv02=-mg?2R
解得:vC=
在C点根据向心力公式得:
N-mg=m
解得:N=
根据牛顿第三定律可知,小球在C点对半圆轨道的压力N′=N=
;
(2)小球从C点抛出后做平抛运动,则
运动时间t=
=2
水平方向做匀速运动,则x=vCt=
?2
答:(1)小球在C点对半圆轨道的压力为
;
(2)小球落到地面上时距离B点的距离为
?2
.
| 1 |
| 2 |
| 1 |
| 2 |
解得:vC=
| v02-4gR |
在C点根据向心力公式得:
N-mg=m
| vC2 |
| R |
解得:N=
| mv02-3mgR |
| R |
根据牛顿第三定律可知,小球在C点对半圆轨道的压力N′=N=
| mv02-3mgR |
| R |
(2)小球从C点抛出后做平抛运动,则
运动时间t=
|
|
水平方向做匀速运动,则x=vCt=
| v02-4gR |
|
答:(1)小球在C点对半圆轨道的压力为
| mv02-3mgR |
| R |
(2)小球落到地面上时距离B点的距离为
| v02-4gR |
|
点评:本题综合运用了动能定理、向心力公式、平抛运动规律,综合性较强,关键理清过程,选择适当的定理或定律进行解题,难度适中.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
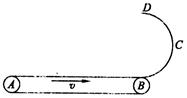
 顺时针匀速转动的传送带,BCD部分为一半径为r、竖直放置的粗糙半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为m的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为
顺时针匀速转动的传送带,BCD部分为一半径为r、竖直放置的粗糙半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为m的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为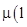 >
>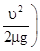 。求:
。求: