题目内容
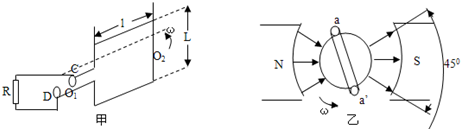
如图 (甲)所示,长L=1m的均匀玻璃管水平放置,左端封闭、右端开口,管内有长为h=15cm的水银柱封住了一段气体A,气柱长LA=40cm,已知大气压强为75cmHg.现把管从水平位置缓慢地转到竖直位置,使开口端向下(水银没溢出),再把它竖直向下缓慢地插入水银槽内,如图(乙)所示,整个过程气体温度不变,当气柱A的长度L'A=37.5cm时,气柱A的压强为 ;此时水银柱下面封住的气柱B的长度为 .
【答案】分析:(1)以A部分气体为研究对象,应用玻意耳定律可以求出气体的压强.
(2)以B部分气体为研究对象,应用玻意耳定律可以求出气体的长度.
解答:解:(1)以A部分气体为研究对象,
pA=75cmHg,VA=LAS=40S,VA′=LA′S=37.5S,
由玻意耳定律得:pAVA=pA′VA′,
即:75×40S=pA′×37.5S,
解得:pA′=80cmHg;
(2)玻璃管竖直放置时,A部分气体,pA1=p-h=60cmHg,
由玻意耳定律得:pAVA=pA1VA1,
即:75×40S=60×LA1S,
解得:LA1=50cm;
B部分气体:pB=75cmHg,VB=LBS=(L-h-LA1)S=35S,
玻璃管插入水银槽后pB′=pA′+h=95cmHg,
由玻意耳定律得:pBVB=pB′VB′,
即:75×35S=95×LB′S,
解得:LB′≈27.63cm;
故答案为:80cmHg;27.63cm.
点评:本题考查了求气体的压强、气柱的长度等问题,理解题意、知道气体状态变化过程,应用玻意耳定律即可正确解题.
(2)以B部分气体为研究对象,应用玻意耳定律可以求出气体的长度.
解答:解:(1)以A部分气体为研究对象,
pA=75cmHg,VA=LAS=40S,VA′=LA′S=37.5S,
由玻意耳定律得:pAVA=pA′VA′,
即:75×40S=pA′×37.5S,
解得:pA′=80cmHg;
(2)玻璃管竖直放置时,A部分气体,pA1=p-h=60cmHg,
由玻意耳定律得:pAVA=pA1VA1,
即:75×40S=60×LA1S,
解得:LA1=50cm;
B部分气体:pB=75cmHg,VB=LBS=(L-h-LA1)S=35S,
玻璃管插入水银槽后pB′=pA′+h=95cmHg,
由玻意耳定律得:pBVB=pB′VB′,
即:75×35S=95×LB′S,
解得:LB′≈27.63cm;
故答案为:80cmHg;27.63cm.
点评:本题考查了求气体的压强、气柱的长度等问题,理解题意、知道气体状态变化过程,应用玻意耳定律即可正确解题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图 (甲)所示,长L=1m的均匀玻璃管水平放置,左端封闭、右端开口,管内有长为h=15cm的水银柱封住了一段气体A,气柱长LA=40cm,已知大气压强为75cmHg.现把管从水平位置缓慢地转到竖直位置,使开口端向下(水银没溢出),再把它竖直向下缓慢地插入水银槽内,如图(乙)所示,整个过程气体温度不变,当气柱A的长度L'A=37.5cm时,气柱A的压强为
如图 (甲)所示,长L=1m的均匀玻璃管水平放置,左端封闭、右端开口,管内有长为h=15cm的水银柱封住了一段气体A,气柱长LA=40cm,已知大气压强为75cmHg.现把管从水平位置缓慢地转到竖直位置,使开口端向下(水银没溢出),再把它竖直向下缓慢地插入水银槽内,如图(乙)所示,整个过程气体温度不变,当气柱A的长度L'A=37.5cm时,气柱A的压强为