题目内容
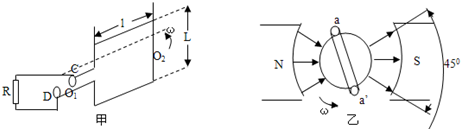
如图(甲)所示,长,宽分别为l和L的矩形线框aa′可绕中心轴O1O2转动,通过电刷C、D跟外电路连接.线框位于如图(乙)所示的区域性辐向磁场中,磁场区域的中心张角为45°,不论线框转到磁场中的什么位置,磁场的方向总是沿着线框平面,磁场中长为l的线框边所在处的磁感应强度大小恒为B,设线框aa’的电阻为r,以角速度ω逆时针匀速转动,电阻R=2r.

(1)求线框aa′转到图(乙)位置时感应电动势的大小;
(2)从线框aa′进入磁场开始计时,作出0~T(T是线框转动周期)时间内通过R的电流iR随时间变化的图象;
(3)求R上的发热功率.

(1)求线框aa′转到图(乙)位置时感应电动势的大小;
(2)从线框aa′进入磁场开始计时,作出0~T(T是线框转动周期)时间内通过R的电流iR随时间变化的图象;
(3)求R上的发热功率.
分析:(1)由题意,磁场的方向总是沿着线框平面,线框总垂直切割磁感线,根据感应电动势公式E=BLv和v=rω结合,求解线框aa′转到图右位置时感应电动势的大小.
(2)线框转动过程中,线框进入磁场切线磁感线作为电源,外接电阻R并联后作为外电路,根据欧姆定律求出电阻R上的电流最大值.从线框aa′进入磁场开始,每转45°,即
周期时间,电流发生一次变化,作出电流的图象.
(3)根据功率公式P=I2R,I是有效值,根据有效值的定义求.
(2)线框转动过程中,线框进入磁场切线磁感线作为电源,外接电阻R并联后作为外电路,根据欧姆定律求出电阻R上的电流最大值.从线框aa′进入磁场开始,每转45°,即
| 1 |
| 8 |
(3)根据功率公式P=I2R,I是有效值,根据有效值的定义求.
解答:解:(1)由题,线框转到磁场中的任何位置时,磁场的方向总是沿着线框平面,则线框切线感线的速度方向始终与磁感线垂直,则感应电动势的大小E=2Blv=2Blω
=BlLω.
(2)线框aa′进入磁场,线框中感应电流为I=
=
.作出电流的图象如图.
(3)设该电流的有效值为I有,根据有效值的定义得
RT=2I2R?
解得,I有=
故R上的发热功率为P=
R=
.
答:
(1)线框aa′转到图(乙)位置时感应电动势的大小为
;
(2)从线框aa′进入磁场开始计时,作出0~T(T是线框转动周期)时间内通过R的电流iR随时间变化的图象如图所示;
(3)R上的发热功率是
.
| L |
| 2 |

(2)线框aa′进入磁场,线框中感应电流为I=
| E |
| R+r |
| BlLω |
| 3r |
(3)设该电流的有效值为I有,根据有效值的定义得
| I | 2 有 |
| T |
| 8 |
解得,I有=
| BlLω |
| 6r |
故R上的发热功率为P=
| I | 2 有 |
| B2l2L2ω2 |
| 12r |
答:
(1)线框aa′转到图(乙)位置时感应电动势的大小为
| BlLω |
| 3r |
(2)从线框aa′进入磁场开始计时,作出0~T(T是线框转动周期)时间内通过R的电流iR随时间变化的图象如图所示;
(3)R上的发热功率是
| B2l2L2ω2 |
| 12r |
点评:本题线框中产生方波,运用法拉第电磁感应定律和欧姆定律即可求得感应电流,容易出错之处在于R的功率,应用有效值求解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图 (甲)所示,长L=1m的均匀玻璃管水平放置,左端封闭、右端开口,管内有长为h=15cm的水银柱封住了一段气体A,气柱长LA=40cm,已知大气压强为75cmHg.现把管从水平位置缓慢地转到竖直位置,使开口端向下(水银没溢出),再把它竖直向下缓慢地插入水银槽内,如图(乙)所示,整个过程气体温度不变,当气柱A的长度L'A=37.5cm时,气柱A的压强为
如图 (甲)所示,长L=1m的均匀玻璃管水平放置,左端封闭、右端开口,管内有长为h=15cm的水银柱封住了一段气体A,气柱长LA=40cm,已知大气压强为75cmHg.现把管从水平位置缓慢地转到竖直位置,使开口端向下(水银没溢出),再把它竖直向下缓慢地插入水银槽内,如图(乙)所示,整个过程气体温度不变,当气柱A的长度L'A=37.5cm时,气柱A的压强为