题目内容
质量m=0.60kg的篮球从距地板H=0.80m高处由静止释放,与水平地板撞击后反弹上升的最大高度h=0.45m,从释放到弹跳至h高处经历的时间t=1.1s.忽略空气阻力,重力加速度取g=10m/s2,求:
(1)篮球下落的时间;
(2)篮球与地板接触时间;
(3)篮球与地板接触过程的平均加速度.
(1)篮球下落的时间;
(2)篮球与地板接触时间;
(3)篮球与地板接触过程的平均加速度.
分析:(1)根据自由落体运动位移时间关系公式列式求解即可;
(2)求解出上抛时间后,用总时间减去上升时间和下降时间即可;
(3)求解出碰撞前后的速度后根据加速度定义公式求解即可.
(2)求解出上抛时间后,用总时间减去上升时间和下降时间即可;
(3)求解出碰撞前后的速度后根据加速度定义公式求解即可.
解答:解:(1)下降过程是自由落体运动,根据位移时间关系公式,有:
H=
g
解得;t1=
=
s=0.4s;
(2)上抛运动的上升过程和下降过程时间相等,故h=
g
,
解得t2=
=
s=0.3s
故碰撞时间为:△t=t-t1-t2=1.1-0.4-0.3=0.4s;
(3)碰撞前速度大小v1=gt1=10×0.4=4m/s;
碰撞后速度大小v2=gt2=10×0.3=3m/s;
规定向下为正,碰撞前速度为正,碰撞后速度为负,则加速度:a=
=
=-17.5/s2;
答:(1)篮球下落的时间为0.4s;
(2)篮球与地板接触时间为0.4s;
(3)篮球与地板接触过程的平均加速度大小为17.5m/s2.
H=
| 1 |
| 2 |
| t | 2 1 |
解得;t1=
|
|
(2)上抛运动的上升过程和下降过程时间相等,故h=
| 1 |
| 2 |
| t | 2 2 |
解得t2=
|
|
故碰撞时间为:△t=t-t1-t2=1.1-0.4-0.3=0.4s;
(3)碰撞前速度大小v1=gt1=10×0.4=4m/s;
碰撞后速度大小v2=gt2=10×0.3=3m/s;
规定向下为正,碰撞前速度为正,碰撞后速度为负,则加速度:a=
| △v |
| △t |
| (-3m/s)-4m/s |
| 0.4s |
答:(1)篮球下落的时间为0.4s;
(2)篮球与地板接触时间为0.4s;
(3)篮球与地板接触过程的平均加速度大小为17.5m/s2.
点评:本题关键明确小球的运动规律,然后选择恰当的运动学公式列式求解,难点是速度变化的矢量性.

练习册系列答案
相关题目
 (2008?茂名一模)如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=0.60kg、速度V0=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L=4R处,重力加速度g取10m/s2,求:
(2008?茂名一模)如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=0.60kg、速度V0=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L=4R处,重力加速度g取10m/s2,求: 如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=3.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=300.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的
如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=3.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=300.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的 (2011?西城区一模)如图,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC.已知滑块的质量m=0.60kg,在A点的速度vA=8.0m/s,AB长x=5.0m,滑块与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2.0m,滑块离开C点后竖直上升h=0.20m,取g=10m/s2.求:
(2011?西城区一模)如图,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC.已知滑块的质量m=0.60kg,在A点的速度vA=8.0m/s,AB长x=5.0m,滑块与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2.0m,滑块离开C点后竖直上升h=0.20m,取g=10m/s2.求: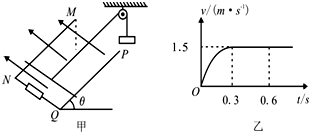 如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=1.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=30°.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的
如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=1.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=30°.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的