题目内容
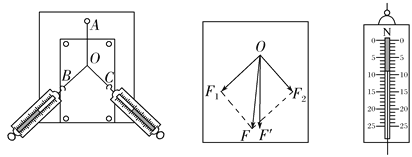
【题目】如图所示，圆形区域内有垂直纸面的匀强磁场，三个质量和电荷量都相同的带电粒子a、b、c，以不同的速率对准圆心O沿着AO方向射入磁场，其运动轨迹如图．若带电粒子只受磁场力的作用，则下列说法正确的是
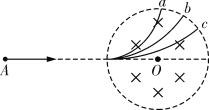
A. a粒子速率最大
B. 它们做圆周运动的周期Ta＜Tb＜Tc
C. c粒子在磁场中运动时间最长
D. c粒子动能最大
【答案】D
【解析】
三个质量和电荷量都相同的带电粒子，以不同的速率垂直进入匀强磁场中，则运动半径的不同，导致运动轨迹也不同．因此运动轨迹对应的半径越大，则粒子的速率也越大．而运动周期它们均一样，但运动时间却由圆弧对应的圆心角决定．
粒子在磁场中做匀速圆周运动时，洛伦兹力提供向心力，由牛顿第二定律得
，解得：
.
A、D、由于三个带电粒子的质量、电荷量均相同，在同一个磁场中，当速度越大时、轨道半径越大，由图示可知，a粒子的轨道半径最小，粒子c的轨道半径最大，则a的粒子速率最小，c粒子的速率最大，c的动能最大，故A错误，D正确；
B、粒子在磁场中做圆周运动的周期：
，由于三个带电粒子的质量、电荷量均相同，在同一个磁场中，粒子的周期T相等，即：Ta=Tb=Tc，故B错误.
C、粒子在磁场中的运动时间
，三粒子运动周期相同，由图示可知，a在磁场中运动的偏转角最大，a的运动时间最长；故C错误.
故选D.
练习册系列答案
相关题目
