Question

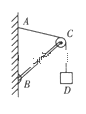
【题目】如图所示，轻杆BC一端用铰链固定于墙上，另一端有一小滑轮C，系重物的轻绳绕过滑轮C将上端固定于墙上的A点，不计摩擦，系统处于静止状态，现将A点沿墙稍上移一些，系统又处于静止状态，则由于A点的上移（　　）

A. 轻杆与竖直墙壁间的夹角减小

B. 绳的拉力增大，轻杆受的压力减小

C. 绳的拉力不变，轻杆受的压力减小

D. 绳的拉力减小，轻杆受的压力不变

Answer 1

【答案】C

【解析】

以滑轮C为研究对象，分析受力情况，系统处于静止状态时，滑轮的合力为零，绳子的拉力大小等于物体的重力，根据平衡条件再分析由于A点的上移时轻杆所受压力的变化情况．

由于绳子的拉力与重力大小相等，由平衡条件得知，轻杆的支持力N与T、G的合力大小相等、方向相反，则轻杆必在T、G的角平分线上，当将A点沿墙稍上移一些，系统又处于静止状态时，根据对称性，可知，T、G夹角增大，则轻杆与竖直墙壁间的夹角增大。故A错误。

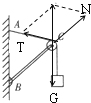
以滑轮C为研究对象，分析受力情况，系统处于静止状态时，滑轮的合力为零，则绳子的拉力T和轻杆的支持力N的合力与重力G大小相等、方向相反，作出力的合成图如图。将A点沿墙稍上移一些时，系统又处于静止状态，则绳子的拉力大小等于物体的重力，保持不变。而轻杆的支持力N大小等于T、G的合力大小，T与G的夹角增大，则知N减小。故绳的拉力不变，轻杆受的压力减小。故C正确，BD错误。故选C。