题目内容
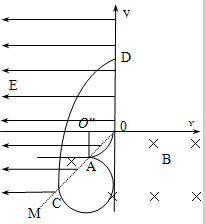
 (2013?兰州模拟)在xOy平面内,第Ⅲ象限内的直线OM是电场与磁场的边界,OM与x轴负方向成45°角.在x<0且OM的左侧空间存在着x轴负方向的匀强电场,场强大小为E=50N/C,在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场,磁感应强度的大小为B=0.2T,如图所示.一不计重力的带负电的微粒,从坐标原点O沿y轴负方向以v0=4×103m/s的初速度进入磁场,已知微粒的带电荷量为q=-4×10-18C,质量为m=1×10-24kg.求:
(2013?兰州模拟)在xOy平面内,第Ⅲ象限内的直线OM是电场与磁场的边界,OM与x轴负方向成45°角.在x<0且OM的左侧空间存在着x轴负方向的匀强电场,场强大小为E=50N/C,在y<0且OM的右侧空间存在着垂直纸面向里的匀强磁场,磁感应强度的大小为B=0.2T,如图所示.一不计重力的带负电的微粒,从坐标原点O沿y轴负方向以v0=4×103m/s的初速度进入磁场,已知微粒的带电荷量为q=-4×10-18C,质量为m=1×10-24kg.求:(1)带电微粒第一次经过磁场边界时的位置坐标及经过磁场边界时的速度方向;
(2)带电微粒最终离开电、磁场区域时的位置坐标;
(3)带电微粒在电、磁场区域运动的总时间(结果可以保留v1=3m/s).
分析:(1)由洛仑兹力充当向心力可得出粒子在转动半径,再由几何关系可得出微粒第一次经过磁场边界时的位置坐标;
(2)粒子进入电场后做类平抛运动,根据类平抛的规律可得出最终离开时的坐标;
(3)根据粒子的运动过程,分别求得电场和磁场中的时间,则可求得总时间.
(2)粒子进入电场后做类平抛运动,根据类平抛的规律可得出最终离开时的坐标;
(3)根据粒子的运动过程,分别求得电场和磁场中的时间,则可求得总时间.
解答:解:
(1)第一次经过磁场边界上的A点,由洛伦兹力公式和牛顿第二定律得:
qv0B=m
,
解得:
r=
=
m=5×10-3m.
A点位置坐标为(-5×10-3m,-5×10-3m).
粒子运动轨迹如图:
可知经过磁场边界时速度方向与OM夹角为450;与电场平行沿x轴负方向.
(2)微粒从C点沿y轴正方向进入电场,做类平抛运动
a=
,
解得:
a=2.0×108m/s2.
由运动学:
△x=
a
=2r,
解得:
t1=1×10-5s.
△y=v0t1.
代入数据解得:
△y=0.04m,
y=△y-2r=(0.04-2×5×10-3)m=3.0×10-2m.
离开电、磁场时的位置D的坐标为(0,3.0×10-2m).
(3)带电微粒在磁场中运动的周期T=
,
在磁场中运动的时间t2=tOA+tAC=
T+
T,
代入数据解得:t2=T=
×10-5s.
带电微粒第一次进入电场中做直线运动的时间
t3=2
=4.0×10-5s,
带电微粒在电、磁场区域运动的总时间
t=t1+t2+t3=(5+
)×10-5s.
答:
(1)带电微粒第一次经过磁场边界时的位置坐标为(-5×10-3m,-5×10-3m),经过磁场边界时的速度方向电场平行沿x轴负方向;
(2)带电微粒最终离开电、磁场区域时的位置坐标为(0,3.0×10-2m);
(3)带电微粒在电、磁场区域运动的总时间(5+
)×10-5s.
(1)第一次经过磁场边界上的A点,由洛伦兹力公式和牛顿第二定律得:
qv0B=m
| ||
| r |
解得:
r=
| mv0 |
| qB |
| 1×10-24×4×103 |
| 4×10-18×0.2 |
A点位置坐标为(-5×10-3m,-5×10-3m).
粒子运动轨迹如图:

可知经过磁场边界时速度方向与OM夹角为450;与电场平行沿x轴负方向.
(2)微粒从C点沿y轴正方向进入电场,做类平抛运动
a=
| qE |
| m |
解得:
a=2.0×108m/s2.
由运动学:
△x=
| 1 |
| 2 |
| t | 2 1 |
解得:
t1=1×10-5s.
△y=v0t1.
代入数据解得:
△y=0.04m,
y=△y-2r=(0.04-2×5×10-3)m=3.0×10-2m.
离开电、磁场时的位置D的坐标为(0,3.0×10-2m).
(3)带电微粒在磁场中运动的周期T=
| 2πm |
| qB |
在磁场中运动的时间t2=tOA+tAC=
| 1 |
| 4 |
| 3 |
| 4 |
代入数据解得:t2=T=
| π |
| 4 |
带电微粒第一次进入电场中做直线运动的时间
t3=2
| v0 |
| a |
带电微粒在电、磁场区域运动的总时间
t=t1+t2+t3=(5+
| π |
| 4 |
答:
(1)带电微粒第一次经过磁场边界时的位置坐标为(-5×10-3m,-5×10-3m),经过磁场边界时的速度方向电场平行沿x轴负方向;
(2)带电微粒最终离开电、磁场区域时的位置坐标为(0,3.0×10-2m);
(3)带电微粒在电、磁场区域运动的总时间(5+
| π |
| 4 |
点评:重点掌握在磁场中运动时几何关系的应用,在电磁场中,运动轨迹的分析能决定题目的成败,同时电场中注意由类平抛运动的规律求解.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
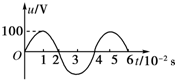
 (2013?兰州模拟)如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( )
(2013?兰州模拟)如图所示,沿x轴正方向传播的一列横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是( ) (2013?兰州模拟)如图所示,有一等腰直角三角形的区域,其斜边长为2L,高为L.在该区域内分布着如图所示的磁场,左侧小三角形内磁场方向垂直纸面向外,右侧小三角形内磁场方向垂直纸面向里,磁感应强度大小均为B.一边长为L、总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则图乙中表示线框中电流i随bc边的位置坐标x变化的图象正确的是( )
(2013?兰州模拟)如图所示,有一等腰直角三角形的区域,其斜边长为2L,高为L.在该区域内分布着如图所示的磁场,左侧小三角形内磁场方向垂直纸面向外,右侧小三角形内磁场方向垂直纸面向里,磁感应强度大小均为B.一边长为L、总电阻为R的正方形导线框abcd,从图示位置开始沿x轴正方向以速度v匀速穿过磁场区域.取沿a→b→c→d→a的感应电流方向为正,则图乙中表示线框中电流i随bc边的位置坐标x变化的图象正确的是( )