题目内容
图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B 两端相距3m ,另一台倾斜,传送带与地面的倾角θ=" 37°," C、D 两端相距4.45m , B、C 相距很近。水平部分AB 以5m/s的速率顺时针转动。将质量为10 kg 的一袋大米放在A 端,到达B 端后,速度大小不变地传到倾斜的CD 部分,米袋与传送带间的动摩擦因数均为0.5。试求:
(1)若CD 部分传送带不运转,求米袋沿传送带所能上升的最大距离。
(2)若要米袋能被送到D 端,求CD 部分顺时针运转的速度应满足的条件及米袋从C 端到D 端所用时间的取值范围。(g=10m/s2 ,sin37°="0.6" , cos37°=0.8)
(1)若CD 部分传送带不运转,求米袋沿传送带所能上升的最大距离。
(2)若要米袋能被送到D 端,求CD 部分顺时针运转的速度应满足的条件及米袋从C 端到D 端所用时间的取值范围。(g=10m/s2 ,sin37°="0.6" , cos37°=0.8)

(1)1.25m
(2)1.16s≤t≤2.1s
⑴米袋在AB上加速时的加速度:
a0=μmg/m=μg=5m/s2①
米袋的速度达到v0=5m/s/时运动的距离:
s0=v02/2a0=2.5m<3m②
因此米袋在达到B点之前就与传送带具有了相同的速度:
设米袋在CD上运动的加速度大小为a,上升的最大距离为smax,由牛顿第二定律得:
a=(mgsinθ+μmgcosθ)/m=10m/s2③
由运动学公式:
smax=v02/(2a)=1.25m④
⑵设CD部分运转速度为v1(v1<5m/s)时米袋恰能到达D点(即米袋到达D点时速度恰好为零),则米袋速度减为v1之前的加速度大小为:
a1=(mgsinθ+μmgcosθ)/m=10m/s2⑤
米袋速度达到
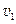 至减为零前的加速度大小为:
至减为零前的加速度大小为:a2=(mgsinθ-μmgcosθ)/m=2m/s2⑥
由运动学公式:
(v02-v12)/(2a1)+v12/(2a2)=4.45⑦
解得v1=4m/s,即要把米袋送到D点,CD部分的速度VCD≥v1=4m/s⑧
米袋恰能运到D点所用时间最长为:
tmax=(v0-v1)/a1+v1/a2=2.1s⑨
若CD部分传送带的速度很大,使米袋沿CD上滑时所受摩擦力一直沿皮带向上,则所用时间最短,此种情况米袋加速度一直为a2。
由SCD=v0tmin-a2tmin2/2⑩
解得tmin=1.16s(用带根式的答案也可)⑾
所以,所求的时间t的范围为1.16s≤t≤2.1s⑿

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (1)这个装置在竖直方向做的运动是匀加速运动吗?是向上运动还是向下运动?
(1)这个装置在竖直方向做的运动是匀加速运动吗?是向上运动还是向下运动? ,已知物块与传送带间的动摩擦因数为
,已知物块与传送带间的动摩擦因数为 ,两皮带轮之间的距离为L=6m,重力加速度
,两皮带轮之间的距离为L=6m,重力加速度 ,求:
,求: ,子弹击中物块后留在其中没有穿出。试求物块被子弹击中到第一次离开皮带的过程中因物块与传送带间的摩擦而产生的热量 。(已知2.02≈2)
,子弹击中物块后留在其中没有穿出。试求物块被子弹击中到第一次离开皮带的过程中因物块与传送带间的摩擦而产生的热量 。(已知2.02≈2)

 的小车停放在光滑水平面上,在小车右端施加一水平恒力F=8N。当小车向右运动速度达到3m/s时,在小车的右端轻放一质量m=2kg的小物块,物
的小车停放在光滑水平面上,在小车右端施加一水平恒力F=8N。当小车向右运动速度达到3m/s时,在小车的右端轻放一质量m=2kg的小物块,物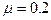 ,假定小车足够长,问:小物块从放在车上开始经过
,假定小车足够长,问:小物块从放在车上开始经过 所通过的位移是多少?(g取
所通过的位移是多少?(g取 )
)





