题目内容
 (2010?闵行区二模)如图所示,小球沿水平面以初速v0通过O点进入半径为R的竖直半圆弧轨道,不计一切阻力.下列说法正确的是( )
(2010?闵行区二模)如图所示,小球沿水平面以初速v0通过O点进入半径为R的竖直半圆弧轨道,不计一切阻力.下列说法正确的是( )分析:小球进入轨道之后,只有重力做功,所以小球的机械能守恒,当恰好能通过最高点时,小球的重力恰好作为向心力,根据向心力的公式可以分析小球的速度的大小,进而可以求得落得动能,离开轨道之后小球做的是平抛运动,由平抛运动的规律可以求得水平方向的位移的大小.
解答:解:A、小球进入竖直半圆弧轨道后做圆周运动运动,但不是匀速圆周运动,由于在上升的过程中,小球的重力要做功,小球的速度的大小在变化,所以不是匀速直线运动,所以A错误.
B、小球在轨道内侧做圆周运动,属于绳的模型,在最高点的最小的速度应该是重力恰好作为小球的向心力,向心力不是零,所以B错误.
C、小球恰能通过半圆弧最高点P,此时的重力恰好作为向心力,由mg=m
,小球从P点到落地的过程中,机械能守恒,所以mg2R+
m
=
mV2,由以上两个等式可以求得小球落地点时的动能为
,所以C正确.
D、小球离开P后做平抛运动,根据平抛运动的规律可得,
水平方向上:x=VPt
竖直方向上:2R=
gt2
并且有 mg=m
,
联立可以解得x=2R,所以D正确.
故选CD.
B、小球在轨道内侧做圆周运动,属于绳的模型,在最高点的最小的速度应该是重力恰好作为小球的向心力,向心力不是零,所以B错误.
C、小球恰能通过半圆弧最高点P,此时的重力恰好作为向心力,由mg=m
| ||
| R |
| 1 |
| 2 |
| V | 2 P |
| 1 |
| 2 |
| 5mgR |
| 2 |
D、小球离开P后做平抛运动,根据平抛运动的规律可得,
水平方向上:x=VPt
竖直方向上:2R=
| 1 |
| 2 |
并且有 mg=m
| ||
| R |
联立可以解得x=2R,所以D正确.
故选CD.
点评:本题属于圆周运动中的绳的模型,刚好能过最高点的条件是球的重力恰好作为向心力,离开轨道之后小球做的是平抛运动.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
 (2010?闵行区二模)如图所示,一段导线abcd位于磁感应强度大小为B的匀强磁场中,且与磁场方向(垂直于纸面向里)垂直.线段ab、bc和cd的长度均为L,且∠abc=∠bcd=135°.流经导线的电流为I,方向如图中箭头所示.导线段abcd所受到的磁场的作用力的合力( )
(2010?闵行区二模)如图所示,一段导线abcd位于磁感应强度大小为B的匀强磁场中,且与磁场方向(垂直于纸面向里)垂直.线段ab、bc和cd的长度均为L,且∠abc=∠bcd=135°.流经导线的电流为I,方向如图中箭头所示.导线段abcd所受到的磁场的作用力的合力( )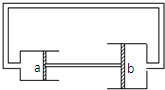 (2010?闵行区二模)如图所示,两个水平相对放置的固定气缸有管道相通,轻质活塞a、b用钢性轻杆固连,可在气缸内无摩擦地移动,两活塞面积分别为Sa和Sb,且Sa<Sb.缸内及管中封有一定质量的气体,整个系统处于平衡状态,大气压强不变.现令缸内气体的温度缓慢升高一点,则系统再次达到平衡状态时( )
(2010?闵行区二模)如图所示,两个水平相对放置的固定气缸有管道相通,轻质活塞a、b用钢性轻杆固连,可在气缸内无摩擦地移动,两活塞面积分别为Sa和Sb,且Sa<Sb.缸内及管中封有一定质量的气体,整个系统处于平衡状态,大气压强不变.现令缸内气体的温度缓慢升高一点,则系统再次达到平衡状态时( )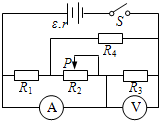 (2010?闵行区二模)如图所示电路中,电源的内电阻为r,R1、R3、R4均为定值电阻,电表均为理想电表.闭合电键S,当滑动变阻器R2的滑动触头P向右滑动时,电表的示数都发生变化,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )
(2010?闵行区二模)如图所示电路中,电源的内电阻为r,R1、R3、R4均为定值电阻,电表均为理想电表.闭合电键S,当滑动变阻器R2的滑动触头P向右滑动时,电表的示数都发生变化,电流表和电压表的示数变化量的大小分别为△I、△U,下列说法正确的是( )