题目内容
【题目】某实验小组在利用单摆测定当地重力加速度的实验中：
（1）摆动时偏角满足的条件是偏角小于5°，为了减小测量周期的误差，计时开始时，摆球应是经过最_____（填“高”或“低”）点的位置。若用L表示摆长，T表示周期，那么重力加速度的表达式为g＝_____。
（2）考虑到单摆振动时空气浮力的影响后，学生甲说：“因为空气浮力与摆球重力方向相反，它对球的作用相当于重力加速度变小，因此振动周期变大。”学生乙说：“浮力对摆球的影响好像用一个轻一些的摆球做实验，因此振动周期不变”，这两个学生中_____。
A．甲的说法正确
B．乙的说法正确
C．两学生的说法都是错误的
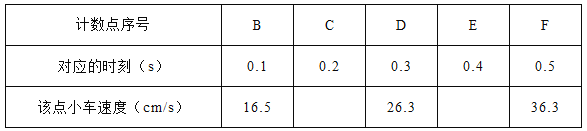
（3）某同学用单摆测当地的重力加速度。他测出了摆线长度L和摆动周期T，如图（a）所示。通过改变悬线长度L，测出对应的摆动周期T，获得多组T与L，再以T2为纵轴、L为横轴画出函数关系图象如图（b）所示。由图象可知，摆球的半径r＝_____m，当地重力加速度g＝_____m/s2；由此种方法得到的重力加速度值与实际的重力加速度值相比会_____（选填“偏大”“偏小”或“一样”）
【答案】低 
A 0.010 9.86 一样
【解析】
（1）单摆测重力加速度时，计时起点应该选取平衡位置即最低点，因为在最高点时，速度为零，误差较大；根据单摆周期公式：
，所以：
（2）根据题意分析，空气对摆球有一个竖直向上的浮力，所以导致竖直方向的合力比重力小，即相当于减小了重力加速度，根据公式，可知单摆的周期变大，甲的说法正确，BC错误A正确
（3）根据
可知：
，，所以图像与横轴交点为半径大小，即
，根据解析式并结合图像可知，图像斜率为：
，解得：
，根据解析式可知，考虑不考虑球的半径，斜率不变都是
，只是图像在坐标系中沿x轴平移，所以此种方法得到的重力加速度值与实际的重力加速度值相比一样。
