题目内容
 如图所示,平行金属板M、N水平放置,电容为C=5.0×10-12F,中央都开有小孔,两极板带等量异种电荷,其电荷量为Q=3.6×10-10C,板间距为d=0.24m.一个质量为m=6×10-6Kg的带电粒子b在两板的正中央位置处于静止状态.另有一个质量也为m=6×10-6Kg的中性粒子a从N板小孔的正下方h=0.28m处以初速度v0=3m/s竖直上抛,两粒子碰后结合为一体.(不计空气阻力,g=10m/s2)求:
如图所示,平行金属板M、N水平放置,电容为C=5.0×10-12F,中央都开有小孔,两极板带等量异种电荷,其电荷量为Q=3.6×10-10C,板间距为d=0.24m.一个质量为m=6×10-6Kg的带电粒子b在两板的正中央位置处于静止状态.另有一个质量也为m=6×10-6Kg的中性粒子a从N板小孔的正下方h=0.28m处以初速度v0=3m/s竖直上抛,两粒子碰后结合为一体.(不计空气阻力,g=10m/s2)求:(1)b粒子所带的电荷量q.
(2)两粒子结合后从极板小孔射出的动能.
分析:(1)带电粒子b原来静止在电容器中,受到的电场力与重力二力平衡,由E=
、U=
求出板间场强E,根据平衡条件即可求得b粒子所带的电荷量q.
(2)a粒子从a到b过程,根据动能定理求出与b粒子前的速度大小.两个粒子碰撞过程遵守动量守恒,即可求出碰后的共同速度.根据动能定理求解两粒子结合后从极板小孔射出的动能.
| U |
| d |
| Q |
| C |
(2)a粒子从a到b过程,根据动能定理求出与b粒子前的速度大小.两个粒子碰撞过程遵守动量守恒,即可求出碰后的共同速度.根据动能定理求解两粒子结合后从极板小孔射出的动能.
解答:解:(1)设两板电势差为U,则由C=
得 U=
=72V
极板间场强为 E=
=300V/m
设粒子带电荷量为q,则有
mg=qE
解得q=2×10-7C
(2)设a粒子与b粒子碰前的速度为v1,则由动能定理得
m
+mg(h+
)=
m
解得v1=1m/s
设两者碰后速度为v2,则有
mv1=2mv2
解得v2=0.5m/s
设两者从M板的小孔射出,则有
-2mg
+qE
=Ek-
(2m)
解得 Ek<0,说明两者不能从M板小孔射出,而从N板的小孔射出.
设从N板小孔射出的速度为v3,则有
2mg
-qE
=Ek-
(2m)
解得Ek=8.7×10-6J
答:(1)b粒子所带的电荷量q是2×10-7C.
(2)两粒子结合后从极板小孔N射出的动能是8.7×10-6J.
| Q |
| U |
| Q |
| C |
极板间场强为 E=
| U |
| d |
设粒子带电荷量为q,则有
mg=qE
解得q=2×10-7C
(2)设a粒子与b粒子碰前的速度为v1,则由动能定理得
| 1 |
| 2 |
| v | 2 1 |
| d |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
解得v1=1m/s
设两者碰后速度为v2,则有
mv1=2mv2
解得v2=0.5m/s
设两者从M板的小孔射出,则有
-2mg
| d |
| 2 |
| d |
| 2 |
| 1 |
| 2 |
| v | 2 2 |
解得 Ek<0,说明两者不能从M板小孔射出,而从N板的小孔射出.
设从N板小孔射出的速度为v3,则有
2mg
| d |
| 2 |
| d |
| 2 |
| 1 |
| 2 |
| v | 2 2 |
解得Ek=8.7×10-6J
答:(1)b粒子所带的电荷量q是2×10-7C.
(2)两粒子结合后从极板小孔N射出的动能是8.7×10-6J.
点评:本题是二力平衡与动能定理的综合,关键要分析出碰后两个粒子从哪个小孔射出,根据动能定理研究.

练习册系列答案
相关题目
 如图所示,平行金属板长L,间距L,两板间存在向下的匀强电场E,一带电粒子(不计重力)沿两板中线以速度V0垂直射入电场,恰好从下板边缘P点射出平行金属板.若将匀强电场换成垂直纸面的匀强磁场,粒子仍然从同一点以同样的速度射入两板间,要粒子同样从P点射出,求:
如图所示,平行金属板长L,间距L,两板间存在向下的匀强电场E,一带电粒子(不计重力)沿两板中线以速度V0垂直射入电场,恰好从下板边缘P点射出平行金属板.若将匀强电场换成垂直纸面的匀强磁场,粒子仍然从同一点以同样的速度射入两板间,要粒子同样从P点射出,求: (2011?吉安模拟)如图所示,平行金属板A、B带有等量异号电荷,电子和质子均以速率v分别从正(A板)、负(B板)两极板上的小孔沿垂直板面的方向射入板间,那么( )
(2011?吉安模拟)如图所示,平行金属板A、B带有等量异号电荷,电子和质子均以速率v分别从正(A板)、负(B板)两极板上的小孔沿垂直板面的方向射入板间,那么( ) 如图所示,平行金属板与水平方向成θ角,板间距离为d,板间电压为U,一质量为m的带电微粒,以水平初速度v0从下板左端边缘进入板间,结果正好沿水平直线通过从上板右端上边缘处射出,求:
如图所示,平行金属板与水平方向成θ角,板间距离为d,板间电压为U,一质量为m的带电微粒,以水平初速度v0从下板左端边缘进入板间,结果正好沿水平直线通过从上板右端上边缘处射出,求: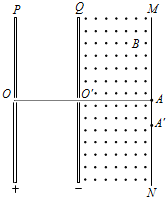 如图所示,平行金属板P、Q的中心分别有小孔O和O′,OO′连线与金属板垂直,两板间的电压为U.在Q板的右侧存在匀强磁场,磁场方向垂直纸面向外,磁感应强度为B.磁场右侧边界处的荧光屏MN与Q板间的距离为L,OO′连线的延长线与MN相交于A点.一质量为m、电荷量为+q的带电粒子,从小孔O处由静止开始运动,通过小孔O′后进入磁场,最终打在MN上的A′点.不计粒子重力.求:
如图所示,平行金属板P、Q的中心分别有小孔O和O′,OO′连线与金属板垂直,两板间的电压为U.在Q板的右侧存在匀强磁场,磁场方向垂直纸面向外,磁感应强度为B.磁场右侧边界处的荧光屏MN与Q板间的距离为L,OO′连线的延长线与MN相交于A点.一质量为m、电荷量为+q的带电粒子,从小孔O处由静止开始运动,通过小孔O′后进入磁场,最终打在MN上的A′点.不计粒子重力.求: 磁流体发电是一项新兴技术,它可以把物体的内能直接转化为电能,如图所示,平行金属板A、B之间相距为d,板间的磁场按匀强磁场处理,磁感应强度为B,等离子体以速度v沿垂直于B的方向射入磁场,金属板A、B是边长为a的正方形,等离子体的电阻率为ρ,外接电阻R.求:
磁流体发电是一项新兴技术,它可以把物体的内能直接转化为电能,如图所示,平行金属板A、B之间相距为d,板间的磁场按匀强磁场处理,磁感应强度为B,等离子体以速度v沿垂直于B的方向射入磁场,金属板A、B是边长为a的正方形,等离子体的电阻率为ρ,外接电阻R.求: