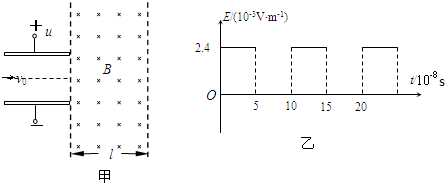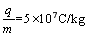题目内容
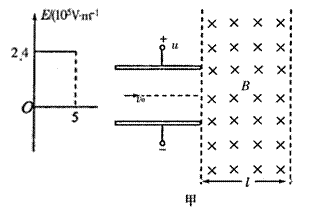
如图甲所示，偏转电场的两个平行极板水平放置，板长L=0.08m，板间距足够大，两板的右侧有水平宽度l=0.06m、竖直宽度足够大的有界匀强磁场．一个比荷为
的带负电粒子以速度v=8×105m/s从两板中间沿与板平行的方向射人偏转电场，若从该粒子进入偏转电场时开始计时，板间场强恰好按图乙所示的规律变化，粒子离开偏转电场后进入匀强磁场并最终垂直磁场右边界射出．不计粒子重力，求：（1）粒子在磁场中运动的速率v；
（2）粒子在磁场中运动的轨道半径R和磁场的磁感应强度B．
【答案】分析：（1）电子在两个平行极板间，水平方向做匀速直线运动，先算出电子在极板间运动的时间，恰好等于偏转电场的一个周期，可知电子先在电场力作用做类平抛运动，后没有电场做匀速直线运动，由牛顿第二定律和运动学公式结合求出带电粒子进入磁场时的速度；
（2）粒子在磁场中，由洛伦兹力提供向心力做匀速圆周运动，画出粒子运动轨迹，根据几何知识求出轨道半径，由牛顿第二定律求解磁感应强度B．
解答：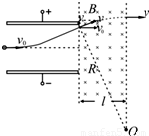
解：（1）根据题意，电子在偏转电场中的运动时间：
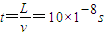…①
对比乙图可知，电子在极板间运动的时间是偏转电场的一个周期．…②
在第一个t=5×l0-8s时间内，电子在垂直于极板方向上做初速度为0的匀加速直线运动，有：
qE=ma…③
v⊥=at…④
在第二个t=5×l0-8s时间内，电子做匀速直线运动，带电粒子进入磁场时的速度为：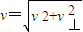
…⑤
联解①③④⑤得：v=1×106m/s…⑥
（2）电子在磁场中，由洛伦兹力提供向心力做匀速圆周运动，作出电子在磁场中的轨迹如图所示；…⑦
设带电粒子在磁场中做匀速圆周运动的半径为R，由几何关系有：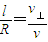
…⑧
粒子在磁场中做匀速圆周运动，由牛顿第二定律有：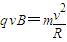
…⑨
联解⑦⑧得：
R=0.1m…⑩
B=0.2T…（11）
答：（1）粒子在磁场中运动的速率v是1×106m/s；
（2）粒子在磁场中运动的轨道半径R是0.1m，磁场的磁感应强度B是0.2T．
点评：本题中电子做类平抛运动时，运用运动的合成与分解法研究，在磁场中做匀速圆周运动时，关键是根据几何知识确定磁场中偏向角与电场中偏向角关系，
（2）粒子在磁场中，由洛伦兹力提供向心力做匀速圆周运动，画出粒子运动轨迹，根据几何知识求出轨道半径，由牛顿第二定律求解磁感应强度B．
解答：
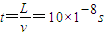解：（1）根据题意，电子在偏转电场中的运动时间：…①对比乙图可知，电子在极板间运动的时间是偏转电场的一个周期．…②
在第一个t=5×l0-8s时间内，电子在垂直于极板方向上做初速度为0的匀加速直线运动，有：
qE=ma…③
v⊥=at…④
在第二个t=5×l0-8s时间内，电子做匀速直线运动，带电粒子进入磁场时的速度为：
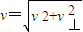…⑤联解①③④⑤得：v=1×106m/s…⑥
（2）电子在磁场中，由洛伦兹力提供向心力做匀速圆周运动，作出电子在磁场中的轨迹如图所示；…⑦
设带电粒子在磁场中做匀速圆周运动的半径为R，由几何关系有：
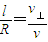…⑧粒子在磁场中做匀速圆周运动，由牛顿第二定律有：
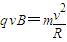…⑨联解⑦⑧得：
R=0.1m…⑩
B=0.2T…（11）
答：（1）粒子在磁场中运动的速率v是1×106m/s；
（2）粒子在磁场中运动的轨道半径R是0.1m，磁场的磁感应强度B是0.2T．
点评：本题中电子做类平抛运动时，运用运动的合成与分解法研究，在磁场中做匀速圆周运动时，关键是根据几何知识确定磁场中偏向角与电场中偏向角关系，
练习册系列答案
快捷英语周周练系列答案
相关题目
的带负电粒子（其重力不计）以v0=8×105m/s速度从两板中间沿与板平行的方向射人偏转电场，进入偏转电场时，偏转电场的场强恰好按图乙所示的规律变化，粒子离开偏转电场后进入匀强磁场，最终垂直磁场右边界射出．求：
