题目内容
(2011?鄂州模拟)如图甲所示,偏转电场的两个平行极板水平放置,板长L=0.08m,板距足够大,两板的右侧有水平宽度l=0.06m、竖直宽度足够大的有界匀强磁场.一个比荷为q/m=5×107 C/kg的粒子(其重力不计)以v0=80m/s速度从两板中间沿与板平行的方向射入偏转电场,进入偏转电场时,偏转电场的场强恰好按图乙开始随时间发生变化,粒子离开偏转电场后进入匀强磁场,最终垂直右边界射出.求:
(1)粒子在磁场中运动的速率v;
(2)粒子在磁场中运动的轨道半径R;
(3)磁场的磁感应强度B;

(1)粒子在磁场中运动的速率v;
(2)粒子在磁场中运动的轨道半径R;
(3)磁场的磁感应强度B;

分析:(1)电子进入平行极板间做类平抛运动,水平方向做匀速直线运动,由t=
求出电子通过极板的时间.电子离开电场时的速度v由水平和竖直两个分速度合成,根据牛顿第二定律和速度公式求出电子离开电场时的速率v,即为粒子在磁场中运动的速率v.
(2)由题粒子进入匀强磁场,最终垂直右边界射出,画出电子在磁场中运动轨迹,由几何知识得知,粒子在磁场中的偏向角等于在电场中的偏向角,由几何关系求出粒子在磁场中运动的轨道半径R.
(3)电子在磁场中由洛伦兹力提供向心力,由牛顿第二定律可求得磁感应强度B.
| l |
| v0 |
(2)由题粒子进入匀强磁场,最终垂直右边界射出,画出电子在磁场中运动轨迹,由几何知识得知,粒子在磁场中的偏向角等于在电场中的偏向角,由几何关系求出粒子在磁场中运动的轨道半径R.
(3)电子在磁场中由洛伦兹力提供向心力,由牛顿第二定律可求得磁感应强度B.
解答:解:(1)电子在偏转电场中的运动时间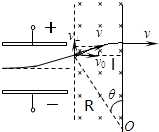
t=
=
s=1.00×10-3 s ①
对比乙图,电子在极板间的时间是偏转电压的一个周期
第一个t=5.00×10-4 s内,电子做类平抛运动,则有
v⊥=
t═60 m/s ②
故v=
=
m/s=1.0×102 m/s ③
(2)电子在磁场中的轨迹如图所示.由题粒子进入匀强磁场,最终垂直右边界射出,由几何知识得知,粒子在磁场中的偏向角等于在电场中的偏向角,设此偏向角为θ.
设电子在磁场中做圆周运动的半径为R.
电子离开电场时,有 sinθ=
在磁场中,有sinθ=
∴
=
④
得 R=
l=
×0.06m=0.1 m ⑤
(3)粒子在磁场中做匀速圆周运动,有 qvB=m
⑥
得B=
=
T=2.0×10-5 T ⑦
答:
(1)粒子在磁场中运动的速率v是1.0×102 m/s;
(2)粒子在磁场中运动的轨道半径R是0.1m;
(3)磁场的磁感应强度B是2.0×10-5 T.

t=
| l |
| v0 |
| 0.08 |
| 80 |
对比乙图,电子在极板间的时间是偏转电压的一个周期
第一个t=5.00×10-4 s内,电子做类平抛运动,则有
v⊥=
| qE |
| m |
故v=
|
| 802+602 |
(2)电子在磁场中的轨迹如图所示.由题粒子进入匀强磁场,最终垂直右边界射出,由几何知识得知,粒子在磁场中的偏向角等于在电场中的偏向角,设此偏向角为θ.
设电子在磁场中做圆周运动的半径为R.
电子离开电场时,有 sinθ=
| v⊥ |
| v |
在磁场中,有sinθ=
| l |
| R |
∴
| l |
| R |
| v⊥ |
| v |
得 R=
| v |
| v⊥ |
| 100 |
| 60 |
(3)粒子在磁场中做匀速圆周运动,有 qvB=m
| v2 |
| R |
得B=
| mv |
| qR |
| 100 |
| 5×107×0.1 |
答:
(1)粒子在磁场中运动的速率v是1.0×102 m/s;
(2)粒子在磁场中运动的轨道半径R是0.1m;
(3)磁场的磁感应强度B是2.0×10-5 T.
点评:本题中电子做类平抛运动时,运用运动的合成与分解法研究,在磁场中做匀速圆周运动时,关键是根据几何知识确定磁场中偏向角与电场中偏向角关系,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?鄂州模拟)负重奔跑是体能训练的常用方式之一,如图所示的装置是运动员负重奔跑的跑步机.已知运动员质量为m1,绳拴在腰间沿水平方向跨过定滑轮(不计滑轮摩擦、质量)悬挂质量为m2的重物,人用力向后蹬,使传送带沿顺时针方向转动,下面说法正确的是( )
(2011?鄂州模拟)负重奔跑是体能训练的常用方式之一,如图所示的装置是运动员负重奔跑的跑步机.已知运动员质量为m1,绳拴在腰间沿水平方向跨过定滑轮(不计滑轮摩擦、质量)悬挂质量为m2的重物,人用力向后蹬,使传送带沿顺时针方向转动,下面说法正确的是( ) (2011?鄂州模拟)质量m=15kg的光滑球A悬空靠在墙和木块B之间,木块B的质量为M=150kg,且静止在水平地板上,如图所示,取g=10m/s2,求:
(2011?鄂州模拟)质量m=15kg的光滑球A悬空靠在墙和木块B之间,木块B的质量为M=150kg,且静止在水平地板上,如图所示,取g=10m/s2,求: