题目内容
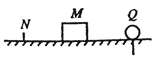
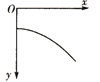
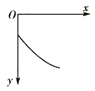
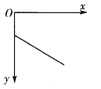
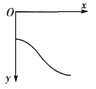
【题目】如图所示,ABCD为固定在竖直平面内的轨道,AB段光滑水平,BC段为光滑圆弧,对应的圆心角θ=37°,半径r=2.5m,CD段平直倾斜且粗糙,各段轨道均平滑连接,倾斜轨道所在区域有场强大小为E=2×l05N/C、方向垂直于斜轨向下的匀强电场.质量m=5×l0﹣2kg、电荷量q=+1×10﹣6C的小物体(视为质点)被弹簧枪发射后,沿水平轨道向左滑行,在C点以速度v0=3m/s冲上斜轨.以小物体通过C点时为计时起点,0.1s以后,场强大小不变,方向反向.已知斜轨与小物体间的动摩擦因数μ=0.25.设小物体的电荷量保持不变,取g=10m/s2.sin37°=0.6,cos37°=0.8.

(1)求弹簧枪对小物体所做的功;
(2)在斜轨上小物体能到达的最高点为P,求CP的长度.
【答案】(1)弹簧枪对小物体所做的功为0.475J;
(2)在斜轨上小物体能到达的最高点为P,CP的长度为0.57m.
【解析】试题分析:(1)设弹簧枪对小物体做功为Wf,由动能定理即可求解;
(2)对小物体进行受力分析,分析物体的运动情况,根据牛顿第二定律求出加速度,结合运动学基本公式即可求解.
解:
(1)设弹簧枪对小物体做功为Wf,由动能定理得Wf﹣mgr(l﹣cosθ)=![]() mv02①
mv02①
代人数据得:Wf=0.475J ②
(2)取沿平直斜轨向上为正方向.设小物体通过C点进入电场后的加速度为a1,
由牛顿第二定律得:﹣mgsinθ﹣μ(mgcosθ+qE)=ma1③
小物体向上做匀减速运动,经t1=0.1s后,速度达到v1,有:v1=v0+a1t1④
由③④可知v1=2.1m/s,设运动的位移为s1,有:sl=v0t1+![]() a1t12⑤
a1t12⑤
电场力反向后,设小物体的加速度为a2,由牛顿第二定律得:
﹣mgsinθ﹣μ(mgcosθ﹣qE)=ma2⑥
设小物体以此加速度运动到速度为0,运动的时间为t2,位移为s2,有:
0=v1+a2t2⑦
s2=v1t2+![]() a2t22⑧
a2t22⑧
设CP的长度为s,有:s=s1+s2⑨
联立相关方程,代人数据解得:s=0.57m
答:(1)弹簧枪对小物体所做的功为0.475J;
(2)在斜轨上小物体能到达的最高点为P,CP的长度为0.57m.