题目内容
在光滑水平面上有一带挡板的长木板,其质量为m,长度为L(挡板的厚度可忽略),木板左端有一质量也是m(可视为质点)的滑块,挡板上固定有一个小炸药包,如下图所示(小炸药包长度以及质量与长木板相比可忽略)滑块与木板间的动摩擦因数恒定,整个系统处于静止。给滑块一个水平向右的初速度v0,滑块相对木板向右运动,刚好能与小炸药包接触,此时小炸药包爆炸(此过程时间极短,爆炸后滑块和木板只在水平方向运动,且完好无损),滑块最终又回到木板的左端,恰与木板相对静止。求:![]()
(1)小炸药包爆炸完毕时,滑块和木板的速度;
(2)从滑块开始运动到最终停在木板左端的整个过程中木板相对地面的位移。
解:(1)设滑块刚要与炸药包接触时的速度为v1对滑块和木板系统在爆炸前:mv0=2mv1①
解得:v1=![]() 水平向右
水平向右
对滑块与木板系统在爆炸前应用功能关系:
μmgL=![]() mv02-
mv02-![]() ×(
×(
设爆炸后滑块和木板的速度分别为v1′,v2′,最终滑块相对静止于木板的左端时速度为v2,系统
在爆炸过程、爆炸前后动量守恒:
mv0=mv1′+mv2′③
mv0=2mv2④
对系统在爆炸后应用功能关系:
μmgL=![]() mv1′2+
mv1′2+![]() mv2′2-
mv2′2-![]() ×(
×(
由②③④⑤解得v1′=0;v2′=v0,水平向右.
(2)爆炸前,对木板应用动能定理:μmgs1=![]() mv12-0⑥
mv12-0⑥
爆炸后,对木板应用动能定理:-μmgs2=![]() mv22-
mv22-![]() mv2′2⑦
mv2′2⑦
所以木板对地的总位移s=s1+s2⑧
由以上各式解得:s=

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
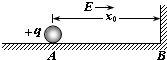 如图所示,在光滑水平面上有一带电量为+q,质量为m的带电小球,置于场强为E、方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设挡板B始终不带电),则第二次碰撞后,小球离开B板的最大距离是( )
如图所示,在光滑水平面上有一带电量为+q,质量为m的带电小球,置于场强为E、方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设挡板B始终不带电),则第二次碰撞后,小球离开B板的最大距离是( ) 如图所示,光滑水平面上静止一带挡板的小车B,其光滑水平表面上放有质量为m的小物块A,A与小车挡板间距为L.现对小物块A始终施加一向右的水平恒力F,当A与挡板相碰后(水平恒力F较小,在碰撞时可忽略),小车B的速度是小物块A碰前的速度的1/3,已知小车B的质量为5m,小物块A始终未从小车上掉下,求
如图所示,光滑水平面上静止一带挡板的小车B,其光滑水平表面上放有质量为m的小物块A,A与小车挡板间距为L.现对小物块A始终施加一向右的水平恒力F,当A与挡板相碰后(水平恒力F较小,在碰撞时可忽略),小车B的速度是小物块A碰前的速度的1/3,已知小车B的质量为5m,小物块A始终未从小车上掉下,求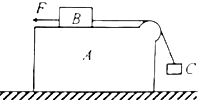 如图,水平面上有一带圆弧形光滑凸起的长方形木块A,木块A上的物体B用轻绳绕过凸起与物体C相连,B与凸起之间的绳是水平的.A与B之间动摩擦因数为μ1=0.8,A与地面之间的动摩擦因数为μ2=0.25.现用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,且C上方的悬线与竖直方向始终成37°角.物体A、B、C的质量分别为m、3m、2m,重力加速度为g,求:
如图,水平面上有一带圆弧形光滑凸起的长方形木块A,木块A上的物体B用轻绳绕过凸起与物体C相连,B与凸起之间的绳是水平的.A与B之间动摩擦因数为μ1=0.8,A与地面之间的动摩擦因数为μ2=0.25.现用一水平向左的拉力F作用在物体B上,恰使物体A、B、C保持相对静止,且C上方的悬线与竖直方向始终成37°角.物体A、B、C的质量分别为m、3m、2m,重力加速度为g,求: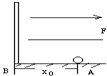 如图,在光滑水平面上有一带电量为-q,质量为m的带电小球,置于场强为E方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设B始终不带电),则第二次碰撞后,小球离开板的最大距离是
如图,在光滑水平面上有一带电量为-q,质量为m的带电小球,置于场强为E方向水平向右的匀强电场中的A处,沿水平方向距A为x0的B处固定一个挡板,释放小球后,小球与挡板发生无能量损失碰撞,若每次碰撞中小球都有一半的电量损失(设B始终不带电),则第二次碰撞后,小球离开板的最大距离是