题目内容
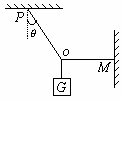
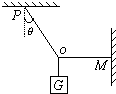如图所示，重15N的物体由OP、OM两条绳拉住，OP与竖直方向成θ角，OM绳始终水平，若OP、OM能承受的最大拉力分别为10| 3 |
分析：先对O点受力分析，受三个拉力，根据平衡条件并运用合成法得到三个力的关系，判断出最先断的绳子，然后求解夹角．
解答：解装置如图，对O点受力分析如图 由图可以看出：sinθ=
假设某时刻OP达到最大拉力
TP=10
N，可求得TM=5
N＜15N
所以此时是绳刚好不被拉断的时刻．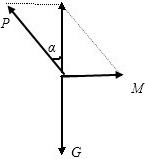
则可得sinθ=
=
即θ=30°
答：绳子OA与竖直方向的夹角α的最大值应为30°．
| TM |
| TP |
假设某时刻OP达到最大拉力
TP=10
| 3 |
| 3 |
所以此时是绳刚好不被拉断的时刻．
则可得sinθ=
5
| ||
10
|
| 1 |
| 2 |
即θ=30°
答：绳子OA与竖直方向的夹角α的最大值应为30°．
点评：本题关键找出各个力的关系，然后根据平衡条件找出临界角度，不难．
练习册系列答案
相关题目
如图所示，在光滑的斜面上，重15N的光滑小球被倾斜的木板挡住处于静止状态，用1厘米长的线段表示5N的力，用作图法求：
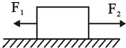如图所示，重为100N的物体放在水平地面，受到水平向左的F1=15N和水平向右的F2=30N两个力的共同作用处于静止，物体与水平面的动摩擦因数μ=0.2，现突然把力F1撤消，则物体受到的摩擦力大小和方向为（ ）| A、20N，水平向左 | B、20N，水平向右 | C、30N，水平向左 | D、30N，水平向右 |
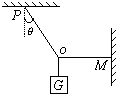如图所示，重15N的物体由OP、OM两条绳拉住，OP与竖直方向成θ角，OM绳始终水平，若OP、OM能承受的最大拉力分别为
N和15N．问为了保持绳不被拉断，θ角的最大值等于多少？
角，若OP、OM能承受的最大拉力分别为
N和15N．问为了保持绳不被拉断，