题目内容
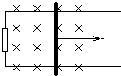 如图,固定于水平地面上接有阻值为R=0.50Ω的电阻的光滑金属框架上放置一金属棒ab,金属框架宽度为L=1.0m,垂直于质量为m=1.0kg的金属棒ab施加一水平恒力F=1.0N,使棒从静止开始运动,当速度达到最大值时,电阻R上产生的焦耳热为Q=0.50J,整个装置处于竖直向下的匀强磁场中,磁感应强度为B=1.0T,金属棒的电阻为r=0.50Ω,不计其它电阻,求:
如图,固定于水平地面上接有阻值为R=0.50Ω的电阻的光滑金属框架上放置一金属棒ab,金属框架宽度为L=1.0m,垂直于质量为m=1.0kg的金属棒ab施加一水平恒力F=1.0N,使棒从静止开始运动,当速度达到最大值时,电阻R上产生的焦耳热为Q=0.50J,整个装置处于竖直向下的匀强磁场中,磁感应强度为B=1.0T,金属棒的电阻为r=0.50Ω,不计其它电阻,求:(1)金属棒的最大速度v;
(2)达到最大速度时金属棒在框架上运动的位移S;
(3)金属棒从静止开始运动到最大速度所需要的时间t.
分析:(1)棒向右做切割磁感线运动,产生感应电流,受到向左的安培力,安培力先小于恒力F,后做恒力F,棒先做加速度减小的变加速运动,后做匀速直线运动,速度达到最大.根据E=BLv、I=
、安培力公式F安=BIL,推导出安培力的表达式,由平衡条件求解最大速度.
(2)根据能量守恒定律求解位移S.
(3)先根据法拉第电磁感应定律求出通过导体棒截面的电荷量,再根据动量定理求解时间t.
| E |
| R+r |
(2)根据能量守恒定律求解位移S.
(3)先根据法拉第电磁感应定律求出通过导体棒截面的电荷量,再根据动量定理求解时间t.
解答:解:(1)当金属棒匀速运动时,速度最大.以最大速度运动时产生的感应电动势为:E=BLv
回路中的感应电流为:I=
达到最大速度时金属棒所受外力与安培力大小相等,即:F=F安=BIL
由以上各式解得金属棒的最大速度为:v=
=
m/s=1m/s
(2)根据能量守恒定律得:FS=Q+
mv2
得:S=
=
=1m
(3)设金属棒从静止开始运动到最大速度通过金属棒的电量为q.
则根据法拉第电磁感应定律:感应电动势平均值为:
=
感应电流的平均值为:
=
电量 q=
△t
联立以上三式得:q=
=
=
C=1C
根据动量定理得:Ft-B
L?△t=mv-0
即得:Ft-BqL=mv
则得:t=
=
s=2s
答:(1)金属棒的最大速度v是1m/s;
(2)达到最大速度时金属棒在框架上运动的位移S是1m;
(3)金属棒从静止开始运动到最大速度所需要的时间t是2s.
回路中的感应电流为:I=
| E |
| R+r |
达到最大速度时金属棒所受外力与安培力大小相等,即:F=F安=BIL
由以上各式解得金属棒的最大速度为:v=
| F(R+r) |
| B2L2 |
| 1×(0.5+0.5) |
| 12×12 |
(2)根据能量守恒定律得:FS=Q+
| 1 |
| 2 |
得:S=
Q+
| ||
| F |
0.5+
| ||
| 1 |
(3)设金属棒从静止开始运动到最大速度通过金属棒的电量为q.
则根据法拉第电磁感应定律:感应电动势平均值为:
. |
| E |
| △Φ |
| △t |
感应电流的平均值为:
. |
| I |
| ||
| R+r |
电量 q=
. |
| I |
联立以上三式得:q=
| △Φ |
| R+r |
| BLS |
| R+r |
| 1×1×1 |
| 0.5+0.5 |
根据动量定理得:Ft-B
. |
| I |
即得:Ft-BqL=mv
则得:t=
| mv+BqL |
| F |
| 1×1+1×1×1 |
| 1 |
答:(1)金属棒的最大速度v是1m/s;
(2)达到最大速度时金属棒在框架上运动的位移S是1m;
(3)金属棒从静止开始运动到最大速度所需要的时间t是2s.
点评:对于电磁感应问题,要正确分析棒的运动情况,掌握E=BLv、I=
、安培力公式F安=BIL,会推导出安培力的表达式.能熟练推导感应电荷量表达式q=
.这些都是常规的思路,关键要熟悉.
| E |
| R+r |
| △Φ |
| R+r |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013?广州三模)如图,相距L的光滑金属导轨,半径为R的
(2013?广州三模)如图,相距L的光滑金属导轨,半径为R的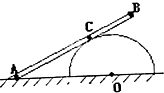 光滑圆柱体固定于水平地面.AB为一均匀直棒,A端放在地上,C点压在柱面上,AB棒处于静止,且AC段长度大于CB段,如图所示,那么直棒AB所受各种作用力的个数是( )
光滑圆柱体固定于水平地面.AB为一均匀直棒,A端放在地上,C点压在柱面上,AB棒处于静止,且AC段长度大于CB段,如图所示,那么直棒AB所受各种作用力的个数是( )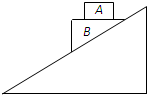 如图,光滑斜面固定于水平地面,滑块A、B叠放后一起由静止开始下滑,在斜面上运动时,A的受力示意图为( )
如图,光滑斜面固定于水平地面,滑块A、B叠放后一起由静止开始下滑,在斜面上运动时,A的受力示意图为( )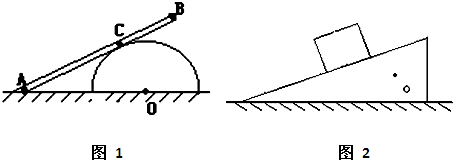
 速直线运动(如图甲).现在该物体A上再放上B物体,但B被嵌在天花板里的黑色铁片挡住(如图乙).则:
速直线运动(如图甲).现在该物体A上再放上B物体,但B被嵌在天花板里的黑色铁片挡住(如图乙).则: