题目内容
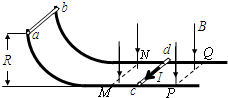
 (2013?广州三模)如图,相距L的光滑金属导轨,半径为R的
(2013?广州三模)如图,相距L的光滑金属导轨,半径为R的| 1 | 4 |
(1)求:ab到达圆弧底端时对轨道的压力大小;
(2)在图中标出ab刚进入磁场时cd棒中的电流方向;
(3)若cd离开磁场时的速度是此刻ab速度的一半,求:cd离开磁场瞬间,ab受到的安培力大小.
分析:(1)根据ab下滑过程中机械能守恒求出ab到达圆弧底端时速度,再由牛顿第二定律求解支持力.
(2)根据右手定则求解.
(3)根据ab、cd组成的系统动量守恒列出等式,根据法拉第电磁感应定律和闭合电路欧姆定律求解.
(2)根据右手定则求解.
(3)根据ab、cd组成的系统动量守恒列出等式,根据法拉第电磁感应定律和闭合电路欧姆定律求解.
解答:(1)设ab到达圆弧底端时受到的支持力大小为N,ab下滑机械能守恒,有:
mgR=
mv2…①
由牛顿第二定律:N-mg=
…②
联立①②得:N=3mg …③
由牛顿第三定律知:对轨道压力大小为N′=3mg…④
(2)根据右手定则得ab刚进入磁场时cd棒中的电流方向如图:
(3)设cd离开磁场时ab在磁场中的速度vab,则cd此时的速度为
vab,
ab、cd组成的系统动量守恒,有:mv=mvab+3m×
vab…⑤
ab、cd构成的闭合回路:
由法拉第电磁感应定律:E=BLvab…⑥
闭合电路欧姆定律:I=
…⑦
安培力公式:Fab=BIL
联立①④⑤⑥⑦得:Fab=
答:(1)ab到达圆弧底端时对轨道的压力大小是3mg;
(2)如上图;
(3)若cd离开磁场瞬间,ab受到的安培力大小是
.
mgR=
| 1 |
| 2 |
由牛顿第二定律:N-mg=
| mv2 |
| R |
联立①②得:N=3mg …③
由牛顿第三定律知:对轨道压力大小为N′=3mg…④
(2)根据右手定则得ab刚进入磁场时cd棒中的电流方向如图:

(3)设cd离开磁场时ab在磁场中的速度vab,则cd此时的速度为
| 1 |
| 2 |
ab、cd组成的系统动量守恒,有:mv=mvab+3m×
| 1 |
| 2 |
ab、cd构成的闭合回路:
由法拉第电磁感应定律:E=BLvab…⑥
闭合电路欧姆定律:I=
| E |
| 2r |
安培力公式:Fab=BIL
联立①④⑤⑥⑦得:Fab=
B2L2
| ||
| 5r |
答:(1)ab到达圆弧底端时对轨道的压力大小是3mg;
(2)如上图;
(3)若cd离开磁场瞬间,ab受到的安培力大小是
B2L2
| ||
| 5r |
点评:本题是电磁感应与电路、磁场、力学等知识的综合应用,根据牛顿第二定律求加速度,以及结合运动学能够分析出金属棒的运动情况.考查分析和处理综合题的能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
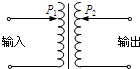 (2013?广州三模)在家用交流稳压器中,变压器的原、副线圈都带有滑动头P1、P2,如图所示.当变压器输入电压发生变化时,可以上下调节P1、P2的位置,使输出电压稳定在220V上.现发现输出电压低于220V,下列措施正确的是( )
(2013?广州三模)在家用交流稳压器中,变压器的原、副线圈都带有滑动头P1、P2,如图所示.当变压器输入电压发生变化时,可以上下调节P1、P2的位置,使输出电压稳定在220V上.现发现输出电压低于220V,下列措施正确的是( )
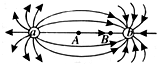 (2013?广州三模)如图所示为点电荷a、b所形成的电场线分布,以下说法正确的是( )
(2013?广州三模)如图所示为点电荷a、b所形成的电场线分布,以下说法正确的是( )