题目内容
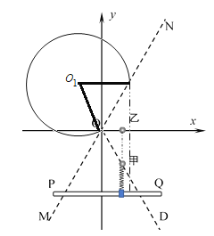
【题目】如图所示，光滑绝缘水平面内有直角坐标系xoy，虚线MN和OD均过O点且都与x轴成60°角。在距x轴为d处平行x轴固定放置一细杆PQ，杆上套有一可以左右滑动的滑块。劲度系数为k、原长为 d 的轻细弹簧垂直于细杆固定在滑块上，另一端放置一质量为 m的绝缘小球甲，小球甲与弹簧不栓接。同时在x轴上、沿着弹簧方向放置一质量为3m、带电量为 – q（q > 0）的小球乙。压缩弹簧将小球甲从OD上某点释放，此后，甲球与乙球发生弹性正碰，小球乙随后进入位于MN左侧的有矩形边界的匀强磁场，磁场方向垂直纸面向外，矩形的一条边与MN重合。改变滑块位置，保证每次小球甲的释放点都在OD上、且滑块与两球在同一条平行于y轴的直线上，并知两球每次都能发生弹性正碰，且碰撞后小球乙的带电量不变，结果发现每次小球乙进入磁场后再离开磁场时的位置是同一点。弹簧始终在弹性限度以内，弹性势能的计算公式是EP =
k·ΔL2，ΔL是弹簧的伸长或缩短量，滑块和小球甲、乙都可视为质点。求：
(1)当滑块的横坐标为
时，小球甲与乙碰前的速度大小；
(2)匀强磁场的磁感应强度B的大小；
(3)若弹簧的最大压缩量为
d，求矩形磁场区域的最小面积。
【答案】(1) 
d；(2)
；(3) 
（2 +
）d 2
【解析】
(1)如图，弹簧的压缩量ΔL与释放点横坐标x之间存在关系式
ΔL =
当横坐标为
d时
释放弹簧后，弹性势能转化为小球甲的动能
k·ΔL02 = mv12
整理得
(2)当粒子释放点坐标为x时，有
小球甲与小球乙发生弹性正碰过程
整理得
乙在磁场中运动时
联立得
由于
因此当x→0时，r→0时，可见，小球乙离开磁场的位置为O点，由几何知识得
r = 2 x
即
整理得
(3)当弹簧最大压缩量为ΔLm =
d 时
最大轨道运动如图所示
最小矩形的长为
a = 2 R
矩形的宽为
矩形面积为
