Question

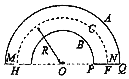
【题目】如图所示，竖直平面内，斜面轨道 AB、水平轨道 BC 、圆弧管道 CDE 及水平轨道 EF 均平滑连接(E 点与 C 点前后错开）已知 A 点到 C 点的水平距离为 L=2m,管道半径 R=0.5m。一个质量 m=1Kg 的小球（其直径略小于管道内径）从 A 点由静止释放，沿 ABCDEF 运动，小球与轨道的 AB 部分和 BC 部分的动摩擦因素μ均为 0.4，其余部分粗糙情况未知。小球到 C 点处的速度为 6m/s；在最高点 D 点时小球对管道的作用力为 8N，最后以 4m/s 的速度在 F 点水平飞出，F 点与落地点 G 的连线与水平面之间的夹角θ＝37°。（g 取 10m/s2）求：

（1）斜面顶端 A 点到水平轨道的高度;

（2）小球在管道最高点 D 点的速度

（3）小球在落地点 G 点的速度

Answer 1

【答案】（1）2.6m ；（2）1m/s或3m/s ；（3）m/s

【解析】

（1）设AB与水平夹角为α，AB水平长度为x1，BC长为x2，对A到C的过程，根据动能定理有：

而

x1+x2=L

代入数据得：

h=2.6m

（2）在D处，因为FND=8N＜mg=10N，所以小球对管道的作用力可能竖直向上，也可能竖直向下，由牛顿第三定律可知管道对小球的作用力可能为竖直向下或竖直向上，有：

管道对小球的作用力为竖直向上时，代入数据得：

vD=1m/s

管道对小球的作用力为竖直向下时有：

代入数据得：

vD=3m/s

（3）设在G处的速度与水平方向的夹角为α，则有：

tanα=2tanθ

vGy=vF2tanθ

得：

vGy=6m/s

由得：