题目内容
3. 如图所示,一质量为1kg的物块滑静止在水平面上的O点,现对物块施加一个与水平面成θ=53°角向下的恒力,物块以3m/s2的加速度向左运动,OP间距为2m,水平面与斜面在P点对接,物块到P点后滑上斜面,不计撞击带来的能量损失,物块滑上倾角为θ=53°角的斜面后推力大小不变,方向变成水平,物块与水平面和斜面的动摩擦因数均为0.5,物块可视为质点,重力加加速度g=10m/s2,sin53°=0.8,cos53°=0.6,求:
如图所示,一质量为1kg的物块滑静止在水平面上的O点,现对物块施加一个与水平面成θ=53°角向下的恒力,物块以3m/s2的加速度向左运动,OP间距为2m,水平面与斜面在P点对接,物块到P点后滑上斜面,不计撞击带来的能量损失,物块滑上倾角为θ=53°角的斜面后推力大小不变,方向变成水平,物块与水平面和斜面的动摩擦因数均为0.5,物块可视为质点,重力加加速度g=10m/s2,sin53°=0.8,cos53°=0.6,求:(1)物块运动到P点时的速度和推力F的大小;
(2)物块在斜面上向上滑行的最大距离.
分析 (1)根据牛顿第二定律求得合外力,应用运动学公式与牛顿第二定律求出物体的速度与力F的大小.
(2)应用牛顿牛顿第二定律和运动学公式可以求出物块向上滑行的最大距离,或应用动能定理求出滑行的最大距离.
解答 解:(1)物块的加速度为3m/s2,根据牛顿第二定律得:F合=ma=3N,
物体在竖直方向:N=Fsinθ+mg,
水平方向:Fcosθ-f=F合,又f=μN,
解得:Fcosθ-μFsinθ-μmg=ma,
代入数据解得:F=40N,
由匀变速直线运动的速度位移公式得:vP2-0=2a•OP,
解得:vP=2$\sqrt{3}$m/s;
(2)物体在斜面上运动时,由牛顿第二定律得:mgsinθ+f-Fcosθ=ma2,
垂直斜面方向上:N=mgcosθ+Fsinθ,又:f=μN,
代入数据解得:a2=3m/s2,方向:平行于斜面向下;
物体在斜面上做匀减速运动,设滑行的最大距离为x2,
由匀变速直线运动的速度位移公式得:0-vP2=2a2x2,
代入数据解得:x2=2m.
答:(1)物块运动到P点时的速度为2$\sqrt{3}$m/s,推力F的大小为40N;
(2)物块在斜面上向上滑行的最大距离为2m.
点评 本题是牛顿第二定律的典型应用题,用好牛顿第二定律和运动学公式是解题的关键,特别注重加速度的方向.

练习册系列答案
相关题目
13. 如图所示,篮球运动员接传来的篮球时,通常要先伸出两臂迎接,手接触到球后,两臂随球迅速引至胸前,这样做可以( )
如图所示,篮球运动员接传来的篮球时,通常要先伸出两臂迎接,手接触到球后,两臂随球迅速引至胸前,这样做可以( )
 如图所示,篮球运动员接传来的篮球时,通常要先伸出两臂迎接,手接触到球后,两臂随球迅速引至胸前,这样做可以( )
如图所示,篮球运动员接传来的篮球时,通常要先伸出两臂迎接,手接触到球后,两臂随球迅速引至胸前,这样做可以( )| A. | 减小篮球的动量的变化量 | |
| B. | 减小篮球对手的冲量 | |
| C. | 减小篮球的动量变化率 | |
| D. | 延长接篮球过程的时间,从而减小篮球的动量变化量 |
14. 为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示,当此车减速上坡时,乘客( )
为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示,当此车减速上坡时,乘客( )
 为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示,当此车减速上坡时,乘客( )
为了让乘客乘车更为舒适,某探究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示,当此车减速上坡时,乘客( )| A. | 受力平衡 | B. | 受到向前的摩擦力作用 | ||
| C. | 所受力的合力沿斜面向上 | D. | 所受力的合力沿斜面向下 |
18. 科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )
科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )
 科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )
科幻电影《星际穿越》中描述了空间站中模拟地球上重力的装置.这个模型可以简化为如图所示的环形实验装置,装置的外侧壁相当于“地板”.让环形实验装置绕O点旋转,能使“地板”上可视为质点的物体在地球表面处有同样的“重力”,已知地球表面重力加速度为g,装置的外半径为R,则旋转角速度应为( )| A. | $\sqrt{\frac{g}{R}}$ | B. | $\sqrt{\frac{R}{g}}$ | C. | 2$\sqrt{\frac{g}{R}}$ | D. | $\sqrt{\frac{2R}{g}}$ |
8. “嫦娥二号”卫星于2010年10月发射成功,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实.若两颗卫星环月飞行均可视为匀速圆周运动,飞行轨道如图所示,则( )
“嫦娥二号”卫星于2010年10月发射成功,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实.若两颗卫星环月飞行均可视为匀速圆周运动,飞行轨道如图所示,则( )
 “嫦娥二号”卫星于2010年10月发射成功,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实.若两颗卫星环月飞行均可视为匀速圆周运动,飞行轨道如图所示,则( )
“嫦娥二号”卫星于2010年10月发射成功,其环月飞行的高度距离月球表面100km,所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实.若两颗卫星环月飞行均可视为匀速圆周运动,飞行轨道如图所示,则( )| A. | “嫦娥二号”环月飞行的周期比“嫦娥一号”更大 | |
| B. | “嫦娥二号”环月飞行的线速度比“嫦娥一号”更大 | |
| C. | “嫦娥二号”环月飞行时角速度比“嫦娥一号”更小 | |
| D. | “嫦娥二号”环月飞行时向心加速度比“嫦娥一号”更小 |
15.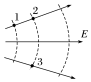 如图所示,实线表示某静电场的电场线,虚线表示该电场的等势线,1、2、3点位置如图.下列判断正确的是( )
如图所示,实线表示某静电场的电场线,虚线表示该电场的等势线,1、2、3点位置如图.下列判断正确的是( )
 如图所示,实线表示某静电场的电场线,虚线表示该电场的等势线,1、2、3点位置如图.下列判断正确的是( )
如图所示,实线表示某静电场的电场线,虚线表示该电场的等势线,1、2、3点位置如图.下列判断正确的是( )| A. | 1、2两点的场强相等 | B. | 1、3两点的场强相等 | ||
| C. | 1、2两点的电势相等 | D. | 2、3两点的电势相等 |
12.下列说法中正确的是( )
| A. | 查德威克在原子核人工转变的实验中发现了中子 | |
| B. | 贝克勒尔通过对天然放射现象的研究发现了原子的核式结构 | |
| C. | 实际上,原子中的电子没有确定的轨道,但在空中各处出现的概率具有一定的规律 | |
| D. | 卢瑟福通过“α粒子散射实验”的研究,发现了原子核是由质子和中子组成的 |
13.如图所示,某人由A点划船渡河,船头指向始终与河岸垂直,则下列说法正确的是( )


| A. | 小船能到达正对岸的B点 | |
| B. | 小船能到达正对岸B点的左侧 | |
| C. | 小船到达对岸的位置与水流速度有关 | |
| D. | 小船到达对岸的时间与水流速度无关 |