题目内容
如图所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为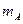 和
和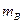 的小物块A和B(可视为质点)分别带有
的小物块A和B(可视为质点)分别带有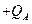 和
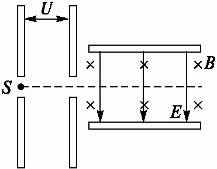
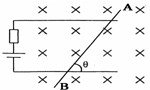
和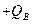 的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B 连接,另一端连接轻质小钩。整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B 、方向水平向里的匀强磁场中。物块A,B 开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面。若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则
的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B 连接,另一端连接轻质小钩。整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B 、方向水平向里的匀强磁场中。物块A,B 开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面。若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则
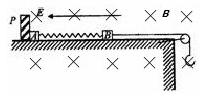
(1)求物块C下落的最大距离;
(2)求小物块C下落到最低点的过程中,小物块B的电势能的变化量、弹簧的弹性势能变化量;
(3)若C的质量改为2M,求小物块A刚离开挡板P时小物块B的速度大小以及此时小物块B对水平桌面的压力.
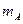 和
和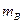 的小物块A和B(可视为质点)分别带有
的小物块A和B(可视为质点)分别带有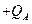 和
和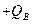 的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B 连接,另一端连接轻质小钩。整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B 、方向水平向里的匀强磁场中。物块A,B 开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面。若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则
的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B 连接,另一端连接轻质小钩。整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B 、方向水平向里的匀强磁场中。物块A,B 开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,物块A、B所带的电荷量不变,B不会碰到滑轮,物块A、B均不离开水平桌面。若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力为零,但不会离开P,则
(1)求物块C下落的最大距离;
(2)求小物块C下落到最低点的过程中,小物块B的电势能的变化量、弹簧的弹性势能变化量;
(3)若C的质量改为2M,求小物块A刚离开挡板P时小物块B的速度大小以及此时小物块B对水平桌面的压力.
(1)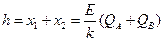 (5分)
(5分)
(2) ;
; (7分)
(7分)
(3) ;
; (8分)
(8分)
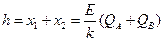 (5分)
(5分)(2)
 ;
; (7分)
(7分)(3)
 ;
; (8分)
(8分)(1)开始时弹簧的形变量为 ,对物体B由平衡条件可得:
,对物体B由平衡条件可得:
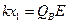 (2分)
(2分)
设A刚离开挡板时,弹簧的形变量为 ,对物块B由平衡条件可得:
,对物块B由平衡条件可得:
 (2分)
(2分)
故C下降的最大距离为: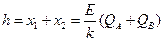 (1分)
(1分)
(2)物块C由静止释放下落 至最低点的过程中,B的电势能增加量为:
至最低点的过程中,B的电势能增加量为: (3分)
(3分)
由能量守恒定律可知:物块由静止释放至下落 至最低点的过程中,c的重力势能减小量等于
至最低点的过程中,c的重力势能减小量等于
B的电势能的增量和弹簧弹性势能的增量即:
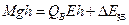 (3分)
(3分)
解得: (1分)
(1分)
(3)当C的质量为2M时,设A刚离开挡板时B的速度为V,由能量守恒定律可知:
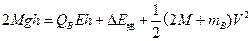 (3分)
(3分)
解得A刚离开P时B的速度为: (1分)
(1分)
因为物块AB均不离开水平桌面,所以对物块B竖直方向受力平衡:
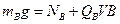 (3分)
(3分)
解得: (1分)
(1分)
 ,对物体B由平衡条件可得:
,对物体B由平衡条件可得: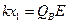 (2分)
(2分)设A刚离开挡板时,弹簧的形变量为
 ,对物块B由平衡条件可得:
,对物块B由平衡条件可得: (2分)
(2分)故C下降的最大距离为:
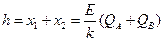 (1分)
(1分)(2)物块C由静止释放下落
 至最低点的过程中,B的电势能增加量为:
至最低点的过程中,B的电势能增加量为: (3分)
(3分)由能量守恒定律可知:物块由静止释放至下落
 至最低点的过程中,c的重力势能减小量等于
至最低点的过程中,c的重力势能减小量等于B的电势能的增量和弹簧弹性势能的增量即:
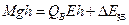 (3分)
(3分)解得:
 (1分)
(1分)(3)当C的质量为2M时,设A刚离开挡板时B的速度为V,由能量守恒定律可知:
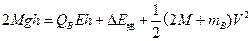 (3分)
(3分)解得A刚离开P时B的速度为:
 (1分)
(1分)因为物块AB均不离开水平桌面,所以对物块B竖直方向受力平衡:
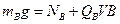 (3分)
(3分)解得:
 (1分)
(1分)
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目

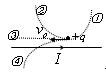
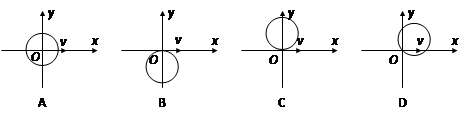
 的绝缘光滑斜面上,整个斜面置于B="0.5" T的匀强磁场中,磁场方向如图所示.物块由静止开始下滑,滑到某一位置时,开始离开斜面(设斜面足够长,g取10 m/s2)。
的绝缘光滑斜面上,整个斜面置于B="0.5" T的匀强磁场中,磁场方向如图所示.物块由静止开始下滑,滑到某一位置时,开始离开斜面(设斜面足够长,g取10 m/s2)。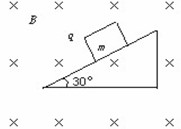
 何种电荷?
何种电荷?