题目内容
（2007?海南）一平行板电容器中存在匀强电场，电场沿竖直方向．两个比荷（即粒子的电荷量与质量之比）不同的带正电的粒子a和b，从电容器的P点（如图）以相同的水平速度射入两平行板之间．测得a和b与电容极板的撞击点到入射点之间的水平距离之比为1：2．若不计重力，则a和b的比荷之比是（ ）分析：粒子的运动方向垂直于电场线的方向，故粒子做类平抛运动，由水平距离之比可求得时间之比；因沿电场线方向粒子的距离相等，则表示出比荷的表达式，求得比荷之比．
解答：解：两带电粒子都做类平抛运动，水平方向匀速运动，有x=vt，垂直金属板方向做初速度为零的匀加速直线运动，有y=
at2，
电荷在电场中受的力为F=Eq，根据牛顿第二定律有F=ma，
联立解得：
=
，因为两粒子在同一电场中运动，E相同，初速度相同，侧位移相同，所以比荷与水平位移的平方成反比．所以比荷之比为4：1，故D正确．
故选D．
| 1 |
| 2 |
电荷在电场中受的力为F=Eq，根据牛顿第二定律有F=ma，
联立解得：
| q |
| m |
| 2yv2 |
| Ex2 |
故选D．
点评：当粒子垂直于电场进入时，粒子做平抛运动，因此可以分为沿电场线的匀加速直线运动和垂直于电场线方向上的匀速直线运动，两个运动互不干扰．
练习册系列答案
阅读快车系列答案
相关题目
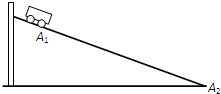（2007?海南）现要验证“当质量一定时，物体运动的加速度与它所受的合外力成正比”这一物理规律．给定的器材如下：一倾角可以调节的长斜面（如图）、小车、计时器一个、米尺．
（2007?海南）如图所示，一辆汽车A拉着装有集装箱的拖车B，以速度v1=30m/s进入向下倾斜的直车道．车道每100m下降2m．为使汽车速度在s=200m的距离内减到v2=10m/s，驾驶员必须刹车．假定刹车时地面的摩擦阻力是恒力，且该力的70%作用于拖车B，30%作用于汽车A．已知A的质量m1=2000kg，B的质量m2=6000kg．求汽车与拖车的连接处沿运动方向的相互作用力．取重力加速度g=10m/s2．
（2007?海南）如图所示，固定在Q点的正点电荷的电场中有M、N两点，已知