题目内容
【题目】如图所示,质量都为m相同的A、B两物块与一劲度系数为k的轻弹簧相连,静止在水平地面上.一块质量也为m橡皮泥C从距A高处由静止下落,与A相碰后立即粘在一起运动且不再分离.当A、C运动到最高点时,物体B恰好对地面无压力.不计空气阻力,且弹簧始终处于弹性限度内,当地的重力加速度为g.求橡皮泥C下落的高度h.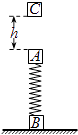
【答案】解:橡皮泥C下落高度h过程机械能守恒,
由机械能守恒定律得:mgh= ![]() mv12 ,
mv12 ,
C与A碰撞过程系统动量守恒,以向下为正方向,
由动量守恒定律得:mv1=(m+m)v2 ,
由平衡条件得:mg=kx,
AC相碰后粘在一起运动,运动到最高点的过程中始末弹性势能相等.
根据系统机械能守恒得: ![]() 2mv22=2mg2x,解得:h=
2mv22=2mg2x,解得:h= ![]() ;
;
答:橡皮泥C下落的高度h为 ![]()
【解析】橡皮泥下落过程机械能守恒,A、C碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律可以求出高度.
【考点精析】掌握机械能守恒及其条件和动量守恒定律是解答本题的根本,需要知道在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变;动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案【题目】在描绘小电珠的伏安特性曲线实验中,一组同学用量程3V的电压表测量小电珠的电压,用多用电表的250mA挡测量通过小电珠的电流.
(1)在图甲电路中,需要将多用电表的两表笔连接到a、b两处.其中黑表笔应与(填“a”或“b”)连接.
(2)将得到的数据记录在表格中,当电压为1.50V时.对应的多用电表指针指示如图乙所示,其读数为 mA.
(3)根据表格中的其他数据,在答题卡的坐标纸上绘制出I﹣U曲线.
电压U/V | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
电流I/mA | 0 | 115 | 154 | 188 | 200 |
(4)由I﹣U曲线可以看出,随电压、电流的增大,小电珠的电阻(填“变大”、“变小”或“不变”).
(5)实验完成后,一位同学用多用电表的欧姆挡测量小电珠的电阻.他将选择开关置于电阻“×l”挡,调零后将红黑表笔接在小电珠的两极上.已知多用电表内部欧姆挡所接电池的电动势为1.5V,欧姆挡刻度盘的中央刻度示数为15.则指针应位于 区间.
A.R>10
B.7<R<9
C.4.5<R<7
D.R<4.5