Question

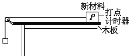
【题目】如图所示，两个等量异种点电荷、固定在同一条水平线上，电荷量分别为和。是水平放置的足够长的光滑绝缘细杆，细杆上套着一个中间穿孔的小球，其质量为，电荷量为（可视为试探电荷，不影响电场的分布）。现将小球从点电荷的正下方点由静止释放，到达点电荷的正下方点时，速度为，为的中点。则（　　）

A.小球从至先做加速运动，后做减速运动

B.小球运动至点时速度为

C.小球最终可能返回至点

D.小球在整个运动过程中的最终速度为

Answer 1

【答案】BD

【解析】

A．根据等量异种点电荷的电场线分布，可知，两点电荷连线的中垂面是等势面，电势为0，正点电荷附近电势大于0，负点电荷附近电势小于0，根据对称关系可得

其中

，

所以小球从C到D运动过程中，只有电场力做功，且由于电势降低，所以电势能减小，电场力做正功，小球在做加速运动，所以A错误；

B．小球由C到D，由动能定理得

则由C到O，由动能定理可得

所以B正确；

C．由分析可知

无穷远处电势也是0，小球由O到D加速运动，再由D到无穷远处，电势升高，电势能增加，电场力做负功，小球做减速运动，所有不可能返回O点，所以C错误；

D．小球从O到无穷远处，电场力做功为0，由能量守恒可知，动能变化量也是0，即无穷远处的速度为

所以D正确。

故选BD。