题目内容
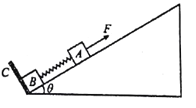
【题目】如图所示,在倾角为e =30。的光滑斜面上有两个用轻质弹簧相连接的物块A、B.它们 的质量均为m,弹簧的劲度系数为k ,C为一固定挡板,系统处于静止状态。现用外力F(恒为 2mg)沿斜面方向拉物块A使之沿斜面向上运动,经过一段时间,物块B刚要与挡板C分离。已知重力加速度为g.则（ ）
A. 从开始到物块B刚要与挡扳C分离的过程,物块A的位移为
B. 物块B刚要离开挡板C时,物块A的加速度为2g
C. 物块B刚要离开挡板C时,物块a的速度为
g
D. 物块B刚要离开挡板C时,物块A的速度为
g
【答案】AC
【解析】开始时系统静止，弹簧处于压缩状态，设此时弹簧压缩量为x1，分析A物体受力可得：kx1=mgsinθ，得：x1=
;在恒力作用下，A向上加速运动，弹簧由压缩状态逐渐变为伸长状态．当B刚要离开C时，弹簧的伸长量设为x2，分析B的受力有：kx2=mgsinθ，得：x2=；所以物块A的位移为：x=x1+x2=
=
，故A正确．设物块B刚要离开挡板C时物块A的加速度为a，由牛顿第二定律有：F-mgsinθ-kx2=ma，结合F=2mg，kx2=mgsinθ，得a=g，故B错误．由于x1=x2，所以初末状态时弹簧的弹性势能相等，对系统，由功能关系得：Fx=mgxsinθ+
mvA2，解得物块B刚要离开挡板C时，物块A的速度为：vA=
g，故C正确，D错误．故选AC.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
