��Ŀ����
1�� ��ͼ��ʾ��PQ��MN�ǹ̶���ˮƽ���ڵ�ƽ�й⻬�������������㹻���������ɺ��Բ��ƣ�������ab��cd���ڹ���ϣ�ʼ���ڹ����ֱ���ҽӴ����ã�������ab��cd��������Ϊm�����Ⱦ�ΪL�����������ij���ǡ�õ��ڹ���ļ�࣬���������γɱպϻ�·��������ab�ĵ���Ϊ2R��������cd�ĵ���ΪR������װ�ô�����ֱ���ϡ��Ÿ�Ӧǿ��ΪB����ǿ�ų��У�
��ͼ��ʾ��PQ��MN�ǹ̶���ˮƽ���ڵ�ƽ�й⻬�������������㹻���������ɺ��Բ��ƣ�������ab��cd���ڹ���ϣ�ʼ���ڹ����ֱ���ҽӴ����ã�������ab��cd��������Ϊm�����Ⱦ�ΪL�����������ij���ǡ�õ��ڹ���ļ�࣬���������γɱպϻ�·��������ab�ĵ���Ϊ2R��������cd�ĵ���ΪR������װ�ô�����ֱ���ϡ��Ÿ�Ӧǿ��ΪB����ǿ�ų��У���1�������ֽ�����ab������ʹ������cd�����䴹ֱ��ˮƽ����F�����£��ع�����ٶ�v�������˶�����֪��Դ�綯�Ƶ��ڵ�Դ�ṩ�ĵ�����ͨ����Դ�ĵ�����ı�ֵ����E=$\frac{{E}_{��}}{q}$���Դ������ĽǶ��Ƶ���֤��������cd�ĸ�Ӧ�綯��E=BLv��
��2�������ڲ����ɵ��ӵĶ����˶��γɵ���������������ʱ������Ͽ�����Ϊ�����ڵ����ɵ��ӵĶ����˶��������ʵģ�����ӵĵ����Ϊe���������cd�����ɵ����ص��߳��ȷ����ܵ���ƽ������f��
��3�����ȱ��ֽ�����ab������ʹ������cd�����䴹ֱ��ˮƽ��F�䣨��Сδ֪�������£��ɾ�ֹ��ʼ�����Լ��ٶ�a���ȼ��ٶ�ֱ���˶���ˮƽ��F������t0ʱ�䳷ȥ������ͬʱ�ͷŽ�����ab����
������F�侭ʱ��t0�Խ�����cdʩ�ӵij�����С��
�����������ڳ�ȥF�����˶������У�ͨ��������cd�ĵ����q��
���� ��1������������ֱ���˶��������밲����ƽ�⣻�ٽ�Ϲ��ܶ���ϵ���������֤����
��2�������ܵ糡���������������������ص��߷�����ֻ�е糡�����������ɹ�����ƽ�������������
��3�������Ƶ�����������ʱ��Ĺ�ϵʽ������ţ�ٵڶ���������F��ʱ��Ĺ�ϵʽ������ͼ��ͼ��ġ���������������ij����������ɼ���֪ʶ��ó�����
�ڸ����������ȷ����������˶���������������������ʽ���ɻ��ֹ��ɿ����λ�Ƶĸı��������ɵ����ļ�����������cd�ĵ������
��� �⣺
��1������������ֱ���˶����������ڰ����������У�
F=BIL
�������غ��֪����������һ�����ڵ�Դ���ṩ�ĵ��ܣ�
����
E��=Fvt��
�綯��E=$\frac{{E}_{��}}{q}$=$\frac{BLItv}{q}$��
�ɵ����Ķ����֪��q=It
������ã�E=BLv��
�ʿ�֤��
��2���綯��E=BLv��
ac�����˵ĵ��ƲU=$\frac{BLv}{3}$��
cd�����˵ĵ��Ʋ�Ϊ��Ucd=$\frac{2BLv}{3}$
�������ܵ��ĵ糡��Bev=f+$\frac{U}{L}$e=f+2$\frac{Bev}{3}$��
�������������˶���������f=$\frac{Bev}{3}$��
��3��CD���и�Ÿ��߲����ĸ�Ӧ�綯��E=Bl1v
ʱ��t�ĸ�Ӧ����I=$\frac{E}{3R}$=$\frac{BLa{t}_{0}}{3R}$
CD���ڼ��ٹ����У�������ţ�ٵڶ����� F-BIl1=ma
��ã�F=$\frac{{B}^{2}{L}^{2}a}{3R}{t}_{0}$+ma
$F=\frac{{{B^2}l_1^2a}}{R}t+ma$
������ʽ���ɵõ�����F��ʱ��仯��ͼ����ͼ��ʾ����ͼ�������֪������ʱ��t0������F�ij���I
I=$\frac{1}{2}$[��$\frac{{B}^{2}{L}^{2}a}{3R}{t}_{0}$+ma+ma]t0
��ã�I=$\frac{{B}^{2}{L}^{2}a{t}_{0}^{2}}{6R}$+mat0
����ӳ�ȥF�䵽ab��cd���ĸպôﵽ��ͬ�ٶȵĹ����е�ijʱ�̣�ab��cd���ٶȲ�Ϊ��v�����ʱ��·�в����ĸ�Ӧ�綯��Ei=$\frac{����}{��t}$=$\frac{BL��x}{��t}$=BL��v
��ʱ��·�еĸ�Ӧ����Ii=$\frac{E}{{R}_{��}}$=$\frac{BL��v}{3R}$
��ʱab�����ܰ�����Fi=BIiL=$\frac{{B}^{2}{L}^{2}��v}{3R}$
��ab�����ݶ��������У�Fi��t=m��v2
�Դӳ�ȥF�䵽ab��cd���պôﵽ��ͬ�ٶȵĹ������
����$\sum_{i=1}^{n}\frac{{B}^{2}{L}^{2}��v}{3R}��{t}_{i}$=mv2����
$\frac{{B}^{2}{L}^{2}}{3R}\sum_{i=1}^{n}��v��{t}_{i}$=$\frac{{B}^{2}{L}^{2}}{3R}$��x=mv2
����v2=$\frac{{v}_{1}}{2}$=$\frac{a{t}_{0}}{2}$
���Խ��������ı�����s=$\frac{3ma{t}_{0}R}{2{B}^{2}{L}^{2}}$
�����ĵ����q=$\overline{I}$t=$\frac{����}{3R��t}��t$=$\frac{B��S}{3R}$=$\frac{ma{t}_{0}}{2BL}$
�𣺣�1��֤�����ϣ�
��2��������СΪ$\frac{Bev}{3}$
��3���ٽ�����ab�����ij���Ϊ$\frac{{B}^{2}{L}^{2}a{t}_{0}^{2}}{6R}$+mat0
�����������ڳ�ȥF�����˶������У�ͨ��������cd�ĵ����qΪ$\frac{ma{t}_{0}}{2BL}$
���� ���⿼�鷨���ڵ�Ÿ�Ӧ���ɡ������غ㶨�ɼ����ܹ�ϵ��Ӧ�ã�Ҫע������ȷӦ����ѧ���ɽ��з�����⣬�籾���а���ͼ��ͻ��ֵĹ��ɣ����DZ����е��ѵ����ڣ�

 ��ͼ��ʾ�����˿��ڵ�U�ιܣ��Ҳ�ֱ������һ���ֿ�����һ��ˮ�������������������������ע��һЩˮ����ƽ���������
��ͼ��ʾ�����˿��ڵ�U�ιܣ��Ҳ�ֱ������һ���ֿ�����һ��ˮ�������������������������ע��һЩˮ����ƽ���������| A�� | �²�����ˮ����A��B�߶Ȳ�h��С | B�� | �²�����ˮ����A��B�߶Ȳ�h���� | ||
| C�� | �Ҳ������������С | D�� | �²�����ˮ����A��B�߶Ȳ�h���� |
| A�� | ����С�������֮��TA��TB=3��2 | B�� | ����С��Ľ��ٶ�֮�Ȧ�A����B=3��2 | ||
| C�� | ����С������ٶ�֮��VA��VB=2��3 | D�� | ����С��İ뾶֮��RA��RB=4��9 |
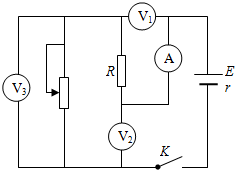 ��ͼ��ʾ����·�ж�ֵ������ֵR���ڵ�Դ������ֵr����������������Ƭ���»����������ѹ��V1��V2��V3ʾ���仯���ľ���ֵ�ֱ�Ϊ��V1����V2����V3�����������Aʾ���仯���ľ���ֵΪ��I��������
��ͼ��ʾ����·�ж�ֵ������ֵR���ڵ�Դ������ֵr����������������Ƭ���»����������ѹ��V1��V2��V3ʾ���仯���ľ���ֵ�ֱ�Ϊ��V1����V2����V3�����������Aʾ���仯���ľ���ֵΪ��I��������| A�� | A��ʾ������ | B�� | V2��ʾ������ | ||
| C�� | ��V3���I�ı�ֵС��r | D�� | ��V1���ڡ�V2 |
 һ����������OΪƽ��λ����A��B֮������г��C��D�ֱ�ΪAO��BO���е㣬��������ΪT��������˵����ȷ���ǣ�������
һ����������OΪƽ��λ����A��B֮������г��C��D�ֱ�ΪAO��BO���е㣬��������ΪT��������˵����ȷ���ǣ�������| A�� | ������A��C��ʱ��Ϊ$\frac{T}{8}$ | |
| B�� | ������C��D��ʱ��Ϊ$\frac{T}{4}$ | |
| C�� | ��A��C��ʱ��Ϊt1��C��O��ʱ��Ϊt2����t1��t2 | |
| D�� | ��Cѡ����Ӧ��t1��t2 |




 ������ͼ��ʾ��װ�ÿ�����֤��е���غ㶨�ɣ�ʵ������Ҫ��������������ͨ����ʱ���ĵ�Դ���ɿ�ֽ����ʹ�������䣮����ʱ������ֽ���ϴ��һϵ�е�С�㣮
������ͼ��ʾ��װ�ÿ�����֤��е���غ㶨�ɣ�ʵ������Ҫ��������������ͨ����ʱ���ĵ�Դ���ɿ�ֽ����ʹ�������䣮����ʱ������ֽ���ϴ��һϵ�е�С�㣮