题目内容
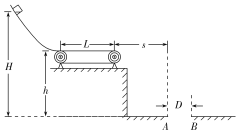
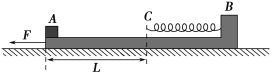
【题目】如图所示,质量M=4 kg的滑板B静止放在光滑水平面上,滑板右端固定一根轻质弹簧,弹簧的自由端C到滑板左端的距离L=0.5 m,可视为质点的小木块A质量m=1 kg,原来静止于滑板的左端,滑板与木块A之间的动摩擦因数μ=0.2。当滑板B受水平向左恒力F=14 N作用时间t后撤去F,这时木块A恰好到达弹簧自由端C处,此后运动过程中弹簧的最大压缩量为s=5 cm。g取10 m/s2。求:
(1)水平恒力F的作用时间t;
(2)木块A压缩弹簧过程中弹簧的最大弹性势能;
(3)当小木块A脱离弹簧且系统达到稳定后,整个运动过程中系统所产生的热量。
【答案】(1)1 s (2)0.3 J (3)1.4 J
【解析】(1)木块A和滑板B均向左做匀加速直线运动,由牛顿第二定律可得
aA=![]() ①
①
aB=![]() ②
②
根据题意有sB-sA=L
即![]() aBt2-
aBt2-![]() aAt2=L③
aAt2=L③
将数据代入①②③联立解得t=1 s
(2)1 s末木块A和滑板B的速度分别为
vA=aAt④
vB=aBt⑤
当木块A和滑板B的速度相同时,弹簧压缩量最大,具有最大弹性势能,根据动量守恒定律有
mvA+MvB=(m+M)v⑥
由能的转化与守恒得
![]() mv
mv![]() +
+![]() Mv=
Mv=![]() (m+M)v2+Ep+μmgs⑦
(m+M)v2+Ep+μmgs⑦
代入数据求得最大弹性势能Ep=0.3 J
(3)二者同速之后,设木块相对木板向左运动离开弹簧后系统又能达到共同速度v′,相对木板向左滑动距离为x,有mvA+MvB=(m+M)v′⑧
由⑧式解得v=v′
由能的转化与守恒定律可得Ep=μmgx⑨
由⑨式解得x=0.15 m
由于s+L>x且x>s,故假设成立
整个过程系统产生的热量为Q=μmg(L+s+x)⑩
由⑩式解得Q=1.4 J

练习册系列答案
相关题目