题目内容
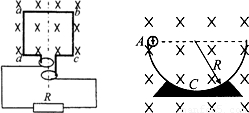
(1)如图所示,线圈abcd的面积是0.05m2,共100匝;线圈总电阻r=1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=
T,线圈以角速度ω=100πrad/s匀速转动.
①若线圈经图示位置时开始计时,写出线圈中感应电动势瞬时值的表达式.
②求通过电阻R的电流有效值.
(2)如图所示,半径为R的绝缘光滑半圆弧轨道固定在竖直平面内,匀强磁场垂直轨道所在的平面,在半圆弧的最低点C接有压力传感器.质量为m、带电量为+q的小球从轨道边缘的A处由静止释放.从传感器传来的数据发现,小球第一次通过C点时对轨道底部的压力恰好为零.重力加速度为g.求匀强磁场的磁感应强度.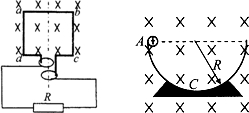
| 1 |
| π |
①若线圈经图示位置时开始计时,写出线圈中感应电动势瞬时值的表达式.
②求通过电阻R的电流有效值.
(2)如图所示,半径为R的绝缘光滑半圆弧轨道固定在竖直平面内,匀强磁场垂直轨道所在的平面,在半圆弧的最低点C接有压力传感器.质量为m、带电量为+q的小球从轨道边缘的A处由静止释放.从传感器传来的数据发现,小球第一次通过C点时对轨道底部的压力恰好为零.重力加速度为g.求匀强磁场的磁感应强度.

(1)①感应电动势最大值为Em=NBSω=100×
×0.05×100V=500V
由于从中性面开始计时,则瞬时值表达式为:e=Emsin(ωt)=500sin(100πt)V
②流过电阻R的最大电流Im=
=
A=50A
通过电阻R的电流有效值I=
Im=25
A
(2)由于洛伦兹力不做功,小球从A运动到C机械能守恒,设到达C点时的速度为v,则有
mgR=
mv2
小球第一次通过C点时对轨道底部的压力恰好为零,则轨道对小球的支持力也为零.
据牛顿第二定律得:
qvB-mg=m
联立以上两式得:B=
答:
(1)①若线圈经图示位置时开始计时,线圈中感应电动势瞬时值的表达式为e=500sin(100πt)V.
②通过电阻R的电流有效值是25
A.
(2)匀强磁场的磁感应强度为
.
| 1 |
| π |
由于从中性面开始计时,则瞬时值表达式为:e=Emsin(ωt)=500sin(100πt)V
②流过电阻R的最大电流Im=
| Em |
| R+r |
| 500 |
| 9+1 |
通过电阻R的电流有效值I=
| ||
| 2 |
| 2 |
(2)由于洛伦兹力不做功,小球从A运动到C机械能守恒,设到达C点时的速度为v,则有
mgR=
| 1 |
| 2 |
小球第一次通过C点时对轨道底部的压力恰好为零,则轨道对小球的支持力也为零.
据牛顿第二定律得:
qvB-mg=m
| v2 |
| R |
联立以上两式得:B=
3m
| ||
| 2qR |
答:
(1)①若线圈经图示位置时开始计时,线圈中感应电动势瞬时值的表达式为e=500sin(100πt)V.
②通过电阻R的电流有效值是25
| 2 |
(2)匀强磁场的磁感应强度为
3m
| ||
| 2qR |

练习册系列答案
相关题目
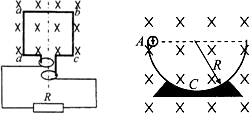 (1)如图所示,线圈abcd的面积是0.05m2,共100匝;线圈总电阻r=1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=
(1)如图所示,线圈abcd的面积是0.05m2,共100匝;线圈总电阻r=1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B= 如图所示,线圈为50匝,在2s内穿过线圈的磁通量由0.02Wb均匀增大到0.06Wb.
如图所示,线圈为50匝,在2s内穿过线圈的磁通量由0.02Wb均匀增大到0.06Wb.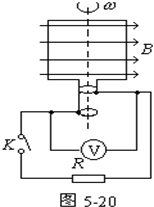 如图所示,线圈的面积100cm2,共100匝.处在B=0.5T的匀强磁场中,以
如图所示,线圈的面积100cm2,共100匝.处在B=0.5T的匀强磁场中,以 T,线圈以角速度ω=100πrad/s匀速转动.
T,线圈以角速度ω=100πrad/s匀速转动.