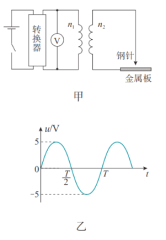
题目内容
【题目】如图所示,一根橡皮绳一端固定于天花板上,另一端连接一质量为m的小球(可视为质点),小球静止时位于O点。现给小球一竖直向下的瞬时速度v0,小球到达的最低点A与O点之间的距离为x。已知橡皮绳中弹力的大小与其伸长量的关系遵从胡克定律。不计橡皮绳的重力及空气阻力。小球运动过程中不会与地板或天花板碰撞。则
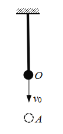
A.小球由O点运动至A点的过程中,天花板对橡皮绳所做的功为![]()
B.小球由O点运动至A点的过程中克服橡皮绳的弹力做功为![]()
C.小球由O点运动至A点的过程中动能先增大后减小
D.小球此后上升至最高点的位置与A点的间距一定等于2x
【答案】B
【解析】
A.小球由O点运动至A点的过程中,天花板对橡皮绳的拉力的位移为零,则天花板对橡皮绳做功为零,选项A错误;
B.小球由O点运动至A点的过程中,根据动能定理
![]()
则克服橡皮绳的弹力做功为
![]()
选项B正确;
C.小球由O点运动至A点的过程中,向上的弹力一直大于向下的重力,则合力方向向上,小球向下做减速运动,小球的动能一直减小,选项C错误;
D.若小球在O点时橡皮绳的伸长量大于或等于x,则由对称性可知,小球此后从A点上升至最高点的位置与A点的间距等于2x;若小球在O点时橡皮绳的伸长量小于x,则小球此后从A点上升至最高点的位置与A点的间距不等于2x;选项D错误。
故选B。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目