题目内容
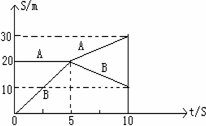
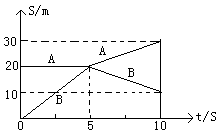
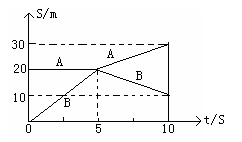
 如图所示,是质量分别为M=1.5kg,m=0.5kg的两个小球A、B在光滑水平面上做对心碰撞前后,画出的位移一时间图象,由图可知下列判断正确的是( )
如图所示,是质量分别为M=1.5kg,m=0.5kg的两个小球A、B在光滑水平面上做对心碰撞前后,画出的位移一时间图象,由图可知下列判断正确的是( )分析:根据x-t图象的斜率等于速度求出各个物体的速度,分别求出碰撞前后的总动量,即可判断动量是否守恒;根据碰撞前后机械能是否守恒判断是否为弹性碰撞即可.
解答:解:A、根据x-t图象可知:A球的初速度为vA=0,B球的初的速度为vB=
=
m/s=4m/s,
碰撞后A球的速度为vA′=
=
=2m/s,碰撞后B球的速度为vB′=
=-2m/s
碰撞前总动量P=MvA+mvB=2kg?m/s,碰撞后总动量P=MvA′+mvB′=2kg?m/s,故两个小球在碰撞前后动量守恒.故A正确.
B、C碰撞过程中,B球的动能变化量为△EkB=
m
-
m
=
×0.5×(22-42)=-3J,即损失3J,故B正确,C错误.
D、A球动能增加量为△EkA=
M
-
M
=
×1.5×22J=3J,则知碰撞前后系统的总动能不变,此碰撞是弹性碰撞,故D正确.
故选ABD
| △xB |
| △t |
| 20 |
| 5 |
碰撞后A球的速度为vA′=
| △xA |
| △t |
| 30-20 |
| 10-5 |
| 10-20 |
| 10-5 |
碰撞前总动量P=MvA+mvB=2kg?m/s,碰撞后总动量P=MvA′+mvB′=2kg?m/s,故两个小球在碰撞前后动量守恒.故A正确.
B、C碰撞过程中,B球的动能变化量为△EkB=
| 1 |
| 2 |
| v | ′2 B |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
D、A球动能增加量为△EkA=
| 1 |
| 2 |
| v | ′2 A |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
故选ABD
点评:本题主要考查了动量守恒定律得应用,要知道判断是否为弹性碰撞的方法是看机械能是否守恒,若守恒,则是弹性碰撞,若不守恒,则不是弹性碰撞.

练习册系列答案
相关题目
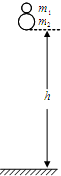 如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )
如图所示,两质量分别为m1和m2的弹性小球又叠放在一起,从高度为h处自由落下,且远大于两小球半径,所有的碰撞都是完全弹性碰撞,且都发生在竖直方向.已知m2=3m1,则小球m1反弹后能达到的高度为( )