题目内容
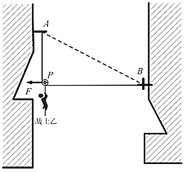
【题目】如图为特种兵过山谷的简化示意图,山谷的两侧为竖直陡崖。将一根不可伸长的细绳两端固定在图中A、B两点。绳上挂一小滑轮P,战士们相互配合,沿着绳子滑到对面。如图所示,战士甲(图中未画出)水平拉住滑轮,质量为70kg的战土乙吊在滑轮上,脚离地处于静止状态,此时AP竖直,PB水平,然后战士甲将滑轮由静止释放,战士乙即可滑到对面公路。不计滑轮大小,也不计绳与滑轮的质量,其中AP=6m,PB=8m,![]() =5.74.求:
=5.74.求:
(1)战士甲释放滑轮前对滑轮的水平拉力F;
(2)若战士乙运动到右侧公路的速率为6m/s,则该过程中克服阻力所做的功;
(3)若战士乙运动到曲线的最低点时速率为7m/s,该处可看做半径R=7m的圆的一部分,则战士乙在最低点时绳AP和PB受到的拉力。
【答案】(1)700N(2)420J(3)725.6N
【解析】
(1)对滑轮受力分析,由平衡条件得:F=T=mg=700N

(2)战士到达右侧时,几何关系如图甲所示,则82+(6+h)2=(14-h)2
解得:h=2.4m
由动能定理得:mgh-Wf=![]()
解得:Wf=420J
(3)战士运动到最低点时,几何关系如图乙所示,则sinθ=![]() =
=![]() ,cosθ=
,cosθ=![]() =0.82
=0.82
在最低点时由牛顿第二定律得:2FTcosθ-mg=m![]()
解得:FT=725.6N
由牛顿第三定律知绳子受到的拉力等于绳子对滑轮的拉力,F′T=FT=725.6N

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目