题目内容
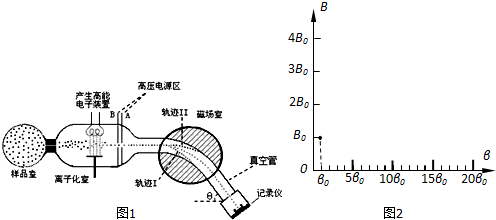
2.质谱仪可以测定有机化合物分子结构,质谱仪的结构如图1所示.有机物的气体分子从样品室注入“离子化”室,在高能电子作用下,样品气体分子离子化或碎裂成离子(如C2H6离子化后得到C2H6+、C2H2+、CH4+等).若离子化后的离子均带一个单位的正电荷e,初速度为零,此后经过高压电源区、圆形磁场室,真空管,最后在记录仪上得到离子,通过处理就可以得到离子质荷比($\frac{m}{e}$),进而推测有机物的分子结构.已知高压电源的电压为U,圆形磁场区的半径为R,真空管与水平面夹角为θ,离子进入磁场室时速度方向指向圆心.(1)请说明高压电源A端应接“正极”还是“负极”,磁场室的磁场方向“垂直纸面向里”还是“垂直纸面向外”;
(2)C2H6+和C2H2+离子同时进入磁场室后,出现了轨迹I和II,试判定它们各自对应的轨迹,并说明原因;
(3)若磁感应强度为B时,记录仪接收到一个明显信号,求与该信号对应的离子质荷比($\frac{m}{e}$);
(4)调节磁场室磁场的大小,在记录仪上可得到不同的离子.设离子的质荷比为β,磁感应强度大小为B,为研究方便可作B-β关系图线.当磁感应强度调至B0时,记录仪上得到的是H+,若H+的质荷比为β0,其B-β关系图线如图2所示,请作出记录仪上得到了CH4+时的B-β的关系图线.
分析 (1)根据正离子在电场中加速确定高压电源A端为正极还是负极.根据左手定则判断磁场的方向.
(2)根据动能定理和洛伦兹力提供向心力得出半径的表达式,结合表达式分析判断.
(3)粒子在磁场中偏转,根据几何关系得出粒子的半径大小,结合半径公式求出该信号对应的离子质荷比.
(4)根据离子质荷比的表达式,得出磁感应强度B与质荷比的关系,从而进行求解.
解答 解:(1)正离子在电场中加速,可知高压电源A端应接“负极”;
根据左手定则知,磁场室的磁场方向应是垂直纸面向外;
(2)设离子通过高压电源后的速度为v,由动能定理可得:
$eU=\frac{1}{2}m{v}^{2}$,
离子在磁场中偏转,洛伦兹力提供向心力,有:
$evB=m\frac{{v}^{2}}{r}$
联立解得:r=$\frac{1}{B}\sqrt{\frac{2mU}{e}}$,
由此可见,质量大的离子的运动轨迹半径大;
${C}_{2}{{H}_{6}}^{+}$对应的轨迹是轨迹Ⅱ;C2H2+对应的轨迹是轨迹Ⅰ.
(3)粒子在磁场中偏转,由几何关系可得:
$r=\frac{R}{tan\frac{θ}{2}}$,
由(2)代入可得:
$\frac{m}{e}=\frac{{B}^{2}{R}^{2}}{2Uta{n}^{2}\frac{θ}{2}}$;
(4)由上题结论知:
$β=\frac{{B}^{2}{R}^{2}}{2Uta{n}^{2}\frac{θ}{2}}$,
得:B=$\frac{tan\frac{θ}{2}}{R}\sqrt{2Uβ}$,
对H+有:${B}_{0}=\frac{tan\frac{θ}{2}}{R}\sqrt{2U{β}_{0}}$,
对$C{{H}_{4}}^{+}$有:β=16β0,
B=$\frac{tan\frac{θ}{2}}{R}\sqrt{2U×16{β}_{0}}=4{B}_{0}$.
故此可得CH4+时的B-β的关系图线如下图所示:
答:(1)高压电源A端应接“负极”;磁场室的磁场方向应是垂直纸面向外.
(2)${C}_{2}{{H}_{6}}^{+}$对应的轨迹是轨迹Ⅱ;C2H2+对应的轨迹是轨迹Ⅰ.
(3)该信号对应的离子质荷比$\frac{m}{e}=\frac{{B}^{2}{R}^{2}}{2Uta{n}^{2}\frac{θ}{2}}$.
(4)如图所示.
点评 本题考查了带电粒子在电场中的加速和磁场中的偏转,结合动能定理和半径公式分析判断,难度中等.

| A. | 阻力 | B. | 弹力 | C. | 支持力 | D. | 浮力 |
| A. | 如果电场线与等势面不垂直,那么电场强度就有一个沿着等势面的分量,在等势面上移动电荷时静电力就要做功,这里用的逻辑方法是归纳法 | |
| B. | 探究作用力与反作用力关系时可以用传感器连在计算机上直接显示力的大小随时间变化的图线,这是物理学中常用的图象法 | |
| C. | 探究加速度与力、质量之间的定量关系,可以在质量一定的情况下,探究物体的加速度与力的关系;再在物体受力一定的情况下,探究物体的加速度与质量的关系,最后归纳出加速度与力、质量之间的关系.这是物理学中常用的控制变量法 | |
| D. | 伽利略采用了以实验检验猜想和假设的科学方法来研究自由落体运动的规律 |
| A. | 任何变化的电场周围一定有磁场 | |
| B. | 物体做受迫振动时,振动稳定后的频率与驱动力频率无关 | |
| C. | 真空中的光速在任何惯性系中测得的数值都相同 | |
| D. | 自感现象是由于导体本身的电流发生变化而产生的电磁感应现象 |
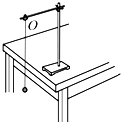 用单摆测定重力加速度的实验装置如图所示.
用单摆测定重力加速度的实验装置如图所示.(1)为了比较准确地测量出当地的重力加速度值,应在下列器材中选用AD(选填选项前的字母).
A.长1m左右的细绳
B.长30cm左右的细绳
C.直径2cm的塑料球
D.直径2cm的铁球
(2)如表是某组同学记录的6组实验数据,并做了部分计算处理.
| 组次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 摆长L/cm | 50.0 | 60.0 | 70.0 | 80.0 | 90.0 | 100.0 |
| 30次全振动的时间t/s | 42.6 | 47.1 | 50.1 | 54.0 | 57.0 | 60.3 |
| 振动周期T/s | 1.42 | 1.57 | 1.67 | 1.80 | 2.01 |
②在计算当地重力加速度g时,以下同学处理数据合理的是C;
A.甲同学利用第六组数据带入单摆周期公式中求出重力加速度g.
B.乙同学分别求出六组摆长的平均值、周期的平均值,然后带入单摆周期公式中求出重力加速度g.
C.丙同学分别把各组数据带入单摆周期公式中求出重力加速度g,然后求g的平均值.
(3)若某同学在实验中没能找到小球,用了一个不规则的小铁块代替小球,因而无法测量摆长的确切值.他第一次用长L1的悬线,测得周期T1;第二次用长L2的悬线,测得周期T2.根据以上数据,该同学能(选填“能”或“不能”)得出当地重力加速度的值,请说明理由.
 把一质量为m的小球放在竖立的弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知A、B的高度差为h,C、B高度差为2h,弹簧的质量和空气的阻力均可忽略,选A位置为重力势能零势能点,则( )
把一质量为m的小球放在竖立的弹簧上,并把球往下按至A的位置,如图甲所示.迅速松手后,弹簧把球弹起,球升至最高位置C(图丙),途中经过位置B时弹簧正好处于自由状态(图乙).已知A、B的高度差为h,C、B高度差为2h,弹簧的质量和空气的阻力均可忽略,选A位置为重力势能零势能点,则( )| A. | 刚松手瞬间,弹簧弹力等于小球重力 | |
| B. | 状态甲中弹簧的弹性势能为2mgh | |
| C. | 状态乙中小球的动能为mgh | |
| D. | 状态丙中系统的机械能为3mgh |

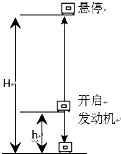 如图为某次太空探测中,科研人员发射星球探测器在最后着陆阶段的示意图,探测器在距星球表面高度为H=20m处悬停(速度为0),首先使探测器在重力作用下自由下落,下落到距地表h高度处开启发动机,使探测器竖直匀减速下降.不计星球表面大气对探测器的阻力影响,星球表面附近的重力加速度为g0=4m/s2.求:
如图为某次太空探测中,科研人员发射星球探测器在最后着陆阶段的示意图,探测器在距星球表面高度为H=20m处悬停(速度为0),首先使探测器在重力作用下自由下落,下落到距地表h高度处开启发动机,使探测器竖直匀减速下降.不计星球表面大气对探测器的阻力影响,星球表面附近的重力加速度为g0=4m/s2.求: