题目内容
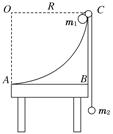
如图甲所示,有一装置由倾斜轨道AB、水平轨道BC、竖直台阶CD和足够长的水平直轨道DE组成,表面处处光滑,且AB段与BC段通过一小圆弧(未画出)平滑相接。有一小球用轻绳竖直悬挂在C点的正上方,小球与BC平面相切但无挤压。紧靠台阶右侧停放着一辆小车,车的上表面水平与B点等高且右侧固定一根轻弹簧,弹簧的自由端在Q点,其中PQ段是粗糙的,Q点右侧表面光滑。现将一个滑块从倾斜轨道的顶端A处自由释放,滑至C点时与小球发生正碰,然后从小车左端P点滑上小车。碰撞之后小球在竖直平面做圆周运动,轻绳受到的拉力如图乙所示。已知滑块、小球和小车的质量分别为m1=3kg、m2=1kg和m3=6kg,AB轨道顶端A点距BC段的高度为h=0.8m,PQ段长度为L=0.4m,轻绳的长度为R=0.5m。 滑块、小球均可视为质点。取g=10m/s2。求:
(1)滑块到达BC轨道上时的速度大小。
(2)滑块与小球碰后瞬间小球的速度大小。
(3)要使滑块既能挤压弹簧,又最终没有滑离小车,则滑块与PQ之间的动摩擦因数μ应在什么范围内?(滑块与弹簧的相互作用始终在弹簧的弹性范围内)
(1)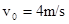 (2)
(2)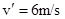 (3)
(3)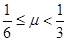
解析试题分析:(1) 设滑块与小球碰撞前瞬间速度为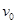 ,由机械能守恒,
,由机械能守恒,
有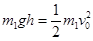 ① (2分)
① (2分)
得 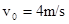 (1分)
(1分)
(2) 设小球在最高点的速度为v,由图乙可知小球在最高点时受到的拉力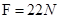 (1分)
(1分)
由牛顿第二定律,有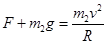 ② (2分)
② (2分)
设小球碰撞后瞬间速度为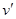 ,由机械能守恒,有
,由机械能守恒,有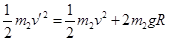 ③ (2分)
③ (2分)
联立①②③并代入数据,解得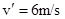 (1分)
(1分)
(3)滑块与小球碰撞过程满足动量守恒: ④
④
得碰撞后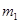 的速度
的速度 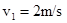 方向向右 (2分)
方向向右 (2分)
滑块最终没有滑离小车,滑块和小车之间必有共同的末速度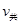
由滑块与小车组成的系统动量守恒: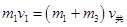 ⑤ (1分)
⑤ (1分)
①若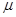 较大,则滑块可能不与弹簧接触就已经与小车相对静止,设滑块恰好滑到Q点,由能量转化与守恒有
较大,则滑块可能不与弹簧接触就已经与小车相对静止,设滑块恰好滑到Q点,由能量转化与守恒有 ⑥ (2分)
⑥ (2分)
联立④⑤⑥得 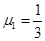
②若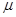 不是很大,则滑块必然挤压弹簧,再被弹回到PQ之间,设滑块恰好回到小车的左端P点处,由能量转化与守恒有
不是很大,则滑块必然挤压弹簧,再被弹回到PQ之间,设滑块恰好回到小车的左端P点处,由能量转化与守恒有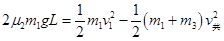 ⑦ (2分)
⑦ (2分)
④⑤⑦得 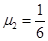
综上所述,得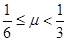 (2分)
(2分)
考点:考查了牛顿第二定律,机械能守恒,动量守恒定律得综合应用

一物体放在升降机底板上,随同升降机由静止开始竖直向下运动,运动过程中物体的机械能与物体位移关系的图象如图所示,其中o- s1过程的图线为曲线,s1-s2过程的图线为直线.根据该图象,下列判断正确的是
A. 过程中物体所受合力一定是变力 过程中物体所受合力一定是变力 |
B. 过程中物体可能在做匀速直线运动 过程中物体可能在做匀速直线运动 |
C. 过程中物体可能在做变加速直线运动 过程中物体可能在做变加速直线运动 |
D. 过程中物体的动能可能在不断增大 过程中物体的动能可能在不断增大 |
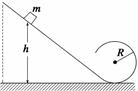
如图所示,运动员把质量为m的足球从水平地面踢出,足球在空中达到的最高点高度为h,在最高点时的速度为v。不计空气阻力,重力加速度为g。下列说法正确的是
A.运动员踢球时对足球做功 |
B.足球上升过程克服重力做功 |
C.运动员踢球时对足球做功 |
D.足球上升过程克服重力做功 |