题目内容
14.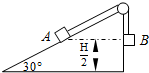 如图,斜面倾角θ=30°,另一边与地面垂直,高为H,斜面顶点有一个定滑轮,物块A和B的质量分别为m1和m2,通过一根不可伸长的细线连结并跨过定滑轮,开始时两物块都位于距地面的垂直距离为$\frac{1}{2}$H的位置上,释放两物块后,A沿斜面无摩擦地上滑,B沿斜面的竖直边下落,且落地后不反弹.若物块A恰好能到达斜面的顶点,试求m1和m2的比值.(滑轮质量、半径及摩擦均忽略)
如图,斜面倾角θ=30°,另一边与地面垂直,高为H,斜面顶点有一个定滑轮,物块A和B的质量分别为m1和m2,通过一根不可伸长的细线连结并跨过定滑轮,开始时两物块都位于距地面的垂直距离为$\frac{1}{2}$H的位置上,释放两物块后,A沿斜面无摩擦地上滑,B沿斜面的竖直边下落,且落地后不反弹.若物块A恰好能到达斜面的顶点,试求m1和m2的比值.(滑轮质量、半径及摩擦均忽略)
分析 开始A、B一起做匀加速运动直到B落地,该过程中系统机械能守恒,当B落地以后,A向上做匀减速运动,最后到达斜面顶端,由机械能守恒定律与动能定理可以求出两物体的质量之比.
解答 解:B下落$\frac{H}{2}$的过程中,A、B组成的系统机械能守恒,由机械能守恒定律得:
m2g$\frac{H}{2}$-m1g$\frac{H}{2}$sinθ=$\frac{1}{2}$(m1+m2)v2-0,
B落地后到A到达斜面顶端过程中,对A由动能定理可得:
-m1g($\frac{H}{2}$-$\frac{H}{2}$sinθ)=0-$\frac{1}{2}$m1v2,
解得:$\frac{{m}_{1}}{{m}_{2}}$=$\frac{1}{2}$;
答:m1和m2的比值是1:2.
点评 分析清楚物体的运动过程,应用机械能守恒定律、动能定理即可正确解题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
4.一个物体在地球表面所受的重力为G,则在距地面高度等于地球半径时,所受引力为( )
| A. | $\frac{G}{2}$ | B. | $\frac{G}{3}$ | C. | $\frac{G}{4}$ | D. | $\frac{G}{9}$ |
2.关于功率,下列各种说法正确的是( )
| A. | 由P=$\frac{W}{t}$可知,只要知道W和t的值就可以计算出任一时刻的功率 | |
| B. | 由功率P=F•v可知,交通工具的牵引力一定与速度成反比 | |
| C. | 由P=$\frac{W}{t}$可知机器做功越多,其功率就越大 | |
| D. | 由P=F•v可知,发动机功率一定时,交通工具的牵引力与运动速度成反比 |
9. 如图所示,长直导线MN被固定,且与线圈A在同一平面内,为了使A中产生逆时针方向的感应电流,可采取的办法是( )
如图所示,长直导线MN被固定,且与线圈A在同一平面内,为了使A中产生逆时针方向的感应电流,可采取的办法是( )
 如图所示,长直导线MN被固定,且与线圈A在同一平面内,为了使A中产生逆时针方向的感应电流,可采取的办法是( )
如图所示,长直导线MN被固定,且与线圈A在同一平面内,为了使A中产生逆时针方向的感应电流,可采取的办法是( )| A. | 闭合电键K | B. | 使线圈A向下平动 | ||
| C. | 把变阻器滑片P向右移动 | D. | 把变阻器滑片P向左移动 |
19.下面有关液体表面张力的说法中错误的是( )
| A. | 在液体表面,分子间的间距大于平衡距离r0,分子间作用力表现为引力 | |
| B. | 液体表面张力使液体表面有收缩的趋势 | |
| C. | 水黾能在水面上行走,这是由于表面张力的缘故 | |
| D. | 小木块能够浮于水面上是液体表面张力与其重力平衡的结果 |
3. 物体A、B质量相同,A放在光滑的水平面上,B放在粗糙的水平面上,在相同的力F作用下,由静止开始都通过了相同的位移s,下列说法错误的是( )
物体A、B质量相同,A放在光滑的水平面上,B放在粗糙的水平面上,在相同的力F作用下,由静止开始都通过了相同的位移s,下列说法错误的是( )
 物体A、B质量相同,A放在光滑的水平面上,B放在粗糙的水平面上,在相同的力F作用下,由静止开始都通过了相同的位移s,下列说法错误的是( )
物体A、B质量相同,A放在光滑的水平面上,B放在粗糙的水平面上,在相同的力F作用下,由静止开始都通过了相同的位移s,下列说法错误的是( )| A. | 力F对A做功较多,做功的平均功率也较大 | |
| B. | 力F对B做功较多,做功的平均功率也较大 | |
| C. | 力F对A、B做的功和做功的平均功率都相同 | |
| D. | 力F对A、B做功相等,但对A做功的平均功率较大 |
4.一定质量气体压强保持不变,当其热力学温度由T变成3T时,其体积由V变成( )
| A. | 3V | B. | 6V | C. | $\frac{V}{3}$ | D. | $\frac{V}{6}$ |
 如图所示,半径为R=0.45m的光滑的$\frac{1}{4}$圆弧轨道AB与粗糙平面BC相连,质量m=2kg的小物块由静止开始从A点滑下,经B点进入动摩擦因数μ=0.2的水平面,最后静止在C点.求:
如图所示,半径为R=0.45m的光滑的$\frac{1}{4}$圆弧轨道AB与粗糙平面BC相连,质量m=2kg的小物块由静止开始从A点滑下,经B点进入动摩擦因数μ=0.2的水平面,最后静止在C点.求: